23. 最小生成树

引：在设计电子电路时，我们常常需要将多个组件的针脚连起。若要连接n个针脚，可以用n-1根连线，我们希望使用的最短的连线来连接针脚。

最小生成树问题：
一个连通无向图$G = (V, E)$中，对于每条边$(u, v) \in E$，为其赋予权重$w(u, v)$。找到一个无环子集$T \subseteq E$，使得所有的结点可以互相到达，并且具有最小的权重，即：$w(T) = \sum_{(u, v) \in T}w(u, v)$的值最小。$T$就是图$G$的最小生成树。

下图中阴影部分组成的就是最小生成树。

生成最小生成树

本章将介绍两种生成最小生成树的算法，他们都用了贪心策略。

思想：创建一个边的集合A，首先讲集合A设置为空集，每次循环加入一条安全的边到集合A中，是的A是最小生成树T的子集，直到集合A覆盖了所有结点。

下面是这个贪心策略的伪代码：

如何找出一个安全的边

这个贪心策略的重点就是如何找出安全的边。

设边集合A覆盖的结点集合为S，没覆盖到的结点集合为V-S。想要生成最小生成树，则必须有且仅有一条边连接S和V-S（连接两个集合的意思为边的一头在S中，另一头在V-S中），所有连接S和V-S的边中权重最小的边就是安全的边。

可以用反证法证明这种选择安全的边的方法是正确的。

Kruskal算法

思想：初始时，将$|V|$个结点视为$|V|$棵树并组成森林。所有边的权重按照从小到大排序，从最小的边开始编译，如果这个边能连接森林中的两棵树，则将这条边加入集合A，并且将这两棵树合并为一棵树。直到森林中只剩一棵树。

伪代码和事例如下：

Prim算法

思想：初始时，给所有的结点赋予一个无穷大的key值，并加入优先队列。每次循环时，从优先队列中取出一个key值最小的结点u加入集合A中，并且更新优先队列中所有与结点u相连的结点v的key值（如果$w(u,v) < v.key$，则$v.key = w(u,v)$）。直到优先队列为空。

伪代码和事例如下：

TODO:时间复杂度分析

留言與分享

22. 基本的图算法

本章介绍图的表示和搜索。
许多的图算法在一开始都会先通过搜索来获得图的结构，其他一些图算法则是对基本的搜索加以优化。
可以说，图的搜索技巧是整个图算法领域的核心。

图的表示

$G = (V, E)$

图G由结点的集合V 和 边的集合E 组成

可以用两种方法表示，一种是邻接链表（下图b），一种是邻接矩阵（下图c）。
邻接链表一般用于表示稀疏图（边数$|E|$远小于$|V|^2$），默认都使用邻接链表表示。在稠密图（$|E|$接近$|V|^2$）的情况下，倾向使用邻接矩阵。

无向图：

有向图：

邻接链表表示

由一个链表数组$Adj$组成，数组大小为$|V|$，链表$Adj[u]$存储了结点$u$出发的边的终点。
比如上面无向图中，从结点1出发有两条边，边的终点分别是2和4，反应到邻接链表中就是$Adj[1]$存储了两个节点2和4。

邻接链表需要的存储空间为$\Theta(|V|+|E|)$

邻接矩阵表示

由一个$|V| \times |V|$ 的矩阵$A = (a_{ij})$表示，并满足以下条件：

$a_{ij} = \left \{ \begin{aligned} & 1 & if (i, j) \in E, &\\ & 0 & other, & \end{aligned} \right.$

当边有权重时，$a_{ij}$可以存储权重值。

邻接矩阵需要的存储空间为$\Theta(|V|^2)$

一些术语

一个结点的出度为，从这个结点触发的边的个数。
一个结点的入度为，到达这个结点的边的个数。

广度优先搜索

思路：利用一个队列，首先将头结点插入队列，循环的取出队列中的一个结点，并将于该结点相连的结点加入队列，直到队列变空，搜索结束。

辅助的给每个结点加入三个属性：

• color：白色表示还未被搜索，灰色表示加入队列，黑色表示从队列里出来
• d：该节点在第几轮被发现
• $\boldsymbol{\pi}$：该结点的前驱（结点第一次被发现时，正在查询的结点）

下面是广度优先搜索的伪代码和事例：

广度优先搜索的正确性

TODO

广度优先搜索的性质

最短路径

从某个结点u做广度优先搜索，可以找出这个结点到其他结点的最短路径。

结点v和结点u的最短路径距离为v.d

从结点v开始 循环列举前驱结点，就是结点v和结点u的最短路径中经过的结点。

广度优先树

广度优先搜算中，我们在$\pi$属性中存储了每个结点的前驱结点，另前驱结点作为该结点的父节点，我们可以得到一个广度优先树。发现新结点的边为树边。

深度优先搜索

思路：尽可能的深入。总是对最近发现的结点v出发的边进行探索，直到结点v出发的边全部被发现时，回溯到v的前驱结点继续探索，直到从源节点出发所有可以到达的结点都被发现。这时如果还有未被搜索的结点，则再随机找一个未被搜索的结点作为源节点进行搜索。

因为可能从一个源节点出发不能搜索到所有结点，所以深度优先搜索会产生多个深度优先树组成深度优先深林。

辅助的给每个结点加入四个属性：

• color：白色表示还未被搜索，灰色表示已被发现但出发的边还没搜索完，黑色表示已被发现并且出发的边已被搜索完
• d：该节点的发现时间
• f：该结点出发搜索结束的时间
• $\boldsymbol{\pi}$：该结点的前驱（结点第一次被发现时，正在查询的结点）

下面是深度优先搜索的伪代码和事例：

结点中的x/y表示该结点的发现时间为x，完成时间为y
图中树边被标记为灰色，向前，横向，向前的边分别被标记为B, C, F

深度优先搜索的性质

括号花定理

如上图b所示，每个结点的发现时间和完成时间组成一个括号花结构。

对于两个结点u和v，如果区间[u.d, u.f] 和 [v.d, v.f] 不相交，则u不是v的后代，v也不是u的后代；
如果[u.d, u.f] 包含在 [v.d, v.f] 内，则u是v后代，反之亦然。

白色路径定理

如果结点v是u的后代，当u.d时间时，存在一条从u到v全部由白色结点组成的路径。

拓扑排序

对于有向无环图$G = (V, E)$，其拓扑排序是G种所有结点的一种线性次序，该次序满足如下条件：如果G包含边(u, v)，则结点u在拓扑排序中处于结点v的前面。

许多实际应用都需要使用有向无环图来说明事件的优先次序。

下图是一个穿衣服的实例，图a中表示了穿戴某一件衣物的依赖关系，图b是图a拓扑排序的结果，按照图b相反的顺序穿衣服就是没问题的了。

拓扑排序的思想为：对图G做DFS，然后按照结点搜索的完成时间逆序排序。伪代码如下：

拓扑排序的正确性：在向无环图中，如果有变(u, v)，那么v肯定比u先完成搜索。

强联通分量

有向图$G = (V, E)$的强连通分量是一个最大结点集合$C \subseteq V$，对于该集合的任意一对结点可以互相到达。

下图a的灰色覆盖区域就是图的强联通分量。

算法伪代码如下：

1. 对G做DFS，并记下每个结点的完成时间u.f
2. 转置G，得到$G^T$，如上图b
3. 按照u.f大小，从大到小对$G^T$做DFS
4. 第三步得到的深度优先深林中，每棵深度优先树的结点都组成为G的一个强联通分量

思想：
  对于分量图$G^{SCC} = (V^{SCC}, E^{SCC})$，$V^{SCC} = {v_1, v_2, ... , v_k}$，图$G$中的强联通分量$C_i$集合代表分量图中的结点$v_i$：如果有$x\in C_i, y\in C_j$，且图$G$中有边$(x, y)$，则边$(v_i, v_j) \in E^{SCC}$，且图$G^{SCC}$是有向无环图。

证明：
  引理1：$C$和$C^\prime$是图$G$的两个强连通分量。当$u, v \in C; u^\prime, v^\prime \in C^\prime$， 若有$u \rightsquigarrow u^\prime$，则不可能有$v^\prime \rightsquigarrow v$。
     可用反证法证明，若有$u \rightsquigarrow u^\prime$且$v^\prime \rightsquigarrow v$，则$C$和$C^\prime$将成为同一个强连通分量。
  引理2：$C$和$C^\prime$是图$G$的两个强连通分量。当$(u, v) \in E$且$u \in C, v \in C^\prime$，则$f(C) > f(C^\prime)$
     当$d(C) < d(C^\prime)$时，若$x$为$C$中最早被发现的结点，则$C$和$C^\prime$中的其它结点都是$x$的子孙，也就是所有结点的完成时间都比$x$早，所以$x.f=f(C)>f(C^\prime)$
     当$d(C) > d(C^\prime)$时，根据引理1，没有从$C$到$C^\prime$的边，也就是$C^\prime$完成之后不会到达任意$C$中的结点，所以$f(C)>f(C^\prime)$
  引理3：$C$和$C^\prime$是图$G$的两个强连通分量。当$(u, v) \in E^T$且$u \in C, v \in C^\prime$，则$f(C) < f(C^\prime)$
     $(u, v) \in E^T \Longrightarrow (v, u) \in E$，由引理2可直接得知$f(C) < f(C^\prime)$
  证明：根据数学归纳法，假设算法第三行所生成的前$k$棵树都是强连通分量，现在需要考虑第$k+1$棵树是否为强连通分量：
     设第$k+1$棵树是$C$，$C$的根节点为$u$，$u$所在的强连通分量为$C^{\prime\prime}$。
     若$G^T$中从$C^{\prime\prime}$到其他强连通分量$C^{\prime\prime\prime}$有边，那么根据引理3可知$f(C^{\prime\prime}) < f(C^{\prime\prime\prime})$。
     而算法对$G^T$做DFS时，是按照$f$大小逆序进行，所以从$C^{\prime\prime}$出来的变都是到前$k$棵树的。
     所以$C=C^{\prime\prime}$，也就是说第$k+1$棵树为强连通分量。

留言與分享

17. 摊还分析

在摊还分析中，我们求数据结构的一个操作序列中所执行的所有操作的平均时间，来评价操作的代价。这样，我们就可以说明一个操作的平均代价是很低的，即使序列中某个单一操作的代价很高。摊还分析不同于平均情况分析，它并不涉及概率，它可以保证最坏情况下每个操作的平均性能。

本章介绍三种摊还分析方法：

• 聚合分析
• 核算法
• 势能法

首先我们先看两个小问题

栈操作

对传统的栈操作MULTIPOP(S, k)扩展，伪代码如下，相当于做k次POP(S)

1
2
3
4

MULTIPOP(S, k)
1   while not STACK-EMPTY(S) and k > 0
2       POP(S)
3       k = k - 1

如果在一个包含s个对象的栈上做MULTIPOP(S, k)操作，POP的次数为min(s, k)。

我们来分析一个由n个PUSH/POP/MULTIPOP组成的操作序列在一个空栈上的执行情况。
MULTIPOP的最坏代价为$O(n)$，那么n个操作的最坏代价是$O(n^2)$吗？

二进制计数器递增

k位二进制计数器递增，初始值为0。用一个位数组A[0…k-1]作为计数器。当计数器保存二级制数x时，x的最低位保存在A[0]中，最高位保存在A[k-1]中，因此$x = \sum\limits_{i=0}^{k-1}A[i]\cdot 2^i$。INCREMENT的伪代码如下：

1
2
3
4
5
6
7

INCREMENT(A)
1   i = 0
2   while i < A.length and A[i] == 1
3       A[i] = 0
4       i = i + 1
5   if i < A.length
6       A[i] = 1

可以想象，最坏情况当k位全部是1时，INCREMENT操作要做k次翻转操作，也就是要花费$\Theta(k)$时间，所以对初值为0的计数器，做n次操作的最坏情况花费$O(nk)$次操作？

从上两个问题，我们都根据一个操作最坏情况的时间消耗推测，整个操作序列的时间消耗，显然不是一个确界。下面我们通过三种摊还分析方法来分析这两个问题中每个操作的平均代价（摊还代价）。

聚合分析

聚合分析——确定n个操作最坏情况的总代价$T(n)$，所以每个操作的平均代价为$T(n)/n$。

栈操作：
虽然单独的MULTIPOP操作可能代价很高，但在一个空栈上实行n个操作，POP和MULTIPOP操作的总消耗最多为O(n)，因为只有push进去数据，POP和MULTIPOP才会有消耗，而且PUSH操作每次只能push一个数据进来。所以n个操作最坏情况的总代价为O(n)，除以n得到每个操作的平均代价为O(1)。

二进制计数器递增：
下图展示了二进制计数器从0递增到16的过程，阴影部分表示递增后需要翻转的位。我们可以发现A[0]每次递增时都发生翻转，A[1]每两次递增发生一次翻转，A[2]每四次递增发生一次翻转，以此类推第i位每$2^i$次递增发生一次翻转。也就是说n次INCREMENT操作后，第i位会翻转$\lfloor n/2^i\rfloor$ 次。
执行n次INCREMENT操作产生的总翻转次数为：

$\sum_{i=0}^{k-1}\lfloor n/2^i\rfloor < n\sum_{i=0}^\infty \frac{1}{2^i} = 2n$

所以，n个INCREMENT操作的最坏情况用时为O(n)，除以n得到每个操作的平均代价为O(1)。

核算法

核算法——对不同的操作赋予不同的费用（可以大于或者小于实际的代价，但不能为负值），称其为摊还代价。当一个操作摊还代价大于实际代价时，我们将差额存起来，称其为信用/存款。后续操作如果有摊还代价小于实际代价时，我们将之前存的信用拿出一部分来抵消这里的差值。如果用$c_i$表示第i个操作的实际代价，用$\hat{c}_i$表示第i个操作的摊还代价，则对任意n个操作的序列，要求：

$\sum_{i=1}^n \hat{c}_i \ge \sum_{i=1}^n c_i$

信用总能刚好抵债或者有剩余，从而使得总的摊还代价为总实际代价的上界。

栈操作：
栈操作的实际代价如下：

1
2
3

PUSH       1
POP        1
MULTIPOP   min(k, s)

我们将栈操作的摊还代价设置为：

1
2
3

PUSH       2
POP        0
MULTIPOP   0

每次PUSH操作支付1的实际代价，剩下的1存起来。存起来的钱和堆栈里的数据量相同，而POP或MULTIPOP操作的实际代价为要pop的数据量，所以存款总能保证大于等于零。
每个操作的摊还代价都是常数，所以总的摊还代价为O(n)。

二进制计数器递增：
将INCREMENT中的操作分为置位操作（第6行，0->1）和复位操作（while循环中的操作，1->0）。令置位操作的摊还代价为2，复位操作的摊还代价为0。每次置位操作可以多出1存起来（存起来的钱和计数器中1的个数相同），复位操作需要预支存款，但复位操作只有当某一位是1的时候才会执行，由于计数器中1的个数永远不会为负，所以存款总能保证大于等于零。
每个操作的摊还代价都是常数，所以总的摊还代价为O(n)。

势能法

势能法将数据结构和势能关联起来——对一个初始化数据结构$D_0$执行n个操作。$c_i$为第i个操作的实际代价，$D_i$为第i次操作后的数据结构。势函数$\Phi$将每个数据结构$D_i$映射到一个实数$\Phi(D_i)$，为数据结构$D_i$的势。第i个操作的摊还代价$\hat{c}_i$用势函数$D_0$定义为：

即，每个操作的摊还代价为实际代价加上操作引起的势变化。所以总摊还代价为：

根据公式1可以得到每个步骤的摊还代价，从而算出总的摊还代价，然后根据公式2可以得出总实际代价的上界/下界（$\Phi(D_n) - \Phi(D_{0})$为正数则得到上界，$\Phi(D_n) - \Phi(D_{0})$为负数则得到下界）。

栈操作：
将势函数定义为当前栈中的数据量。
PUSH操作会压入一个数据，所以势差为1，而且实际代价为1，所以PUSH操作的摊还代价为2。
POP/MULTIPOP操作会弹出x个对象，所以势差为-x，而实际代价为x，所以POP/MULTIPOP操作的摊还代价为0。

栈每个操作的摊还代价都是O(1)，所以n个操作的总摊还代价为O(n)。由于初始的栈为空，而结束时栈的数据量大于等于0，也就是说$\Phi(D_n) - \Phi(D_{0})$为正数，所以n个操作的总摊还代价为总实际代价的上界O(n)。

二进制计数器递增：
将势函数定义为计数器中1的个数$b_i$。
假设第i个操作将$t_i$个位复位，则实际代价为$t_i + 1$，因为还有一次置位操作。
再来考虑摊还代价，如果$b_i$为0，则将k位都复位了，因此$b_{i-1} = t_i = k$。
如果$b_i>0$，则$b_i = b_{i-1} - t_i + 1$。无论那种情况都有$b_i \le b_{i-1} - t_i + 1$，所以摊还代价为：

$\hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1}) \le (t_i + 1) + (-t_i + 1) = 2$

所以总摊还代价的上界为O(n)，由于计数器初始状态为0，而1的个数不会为负数，所以n个操作的总摊还代价为总实际代价的上界O(n)。

势能法的还有个优势就是，我们可以简单的得出当初始状态不是0时实际代价的上界。由公式2可得：

$\sum_{i=1}^n c_i \le \sum_{i=1}^n 2 - b_n + b_0 = 2n -b_n + b_0 \le 2n + b_0 \le 2n + k$

所以只要$k=O(n)$那么总实际代价就是O(n)。

动态表

11章介绍了散列表，我们知道散列表的大小和数据量应该是线性相关的，数据太稀疏会浪费空间，数据太稠密会浪费时间。当我们不知道会有多少数据插入时，就没办法确定散列表的大小，所以要引进动态表。
表扩张——当插入数据时发现散列表的装载因子为1（表的大小和数据量相同），对表进行扩张，比如扩张为两倍大小，首先创建一个两倍大小的表，将原来散列表中的数据插入新创建的表中，然后插入新的数据，最后不能忘了把老的表析构。

表收缩——当删除数据时发现散列包的装载因子小于某个值，对表进行收缩，与表的扩张类似，比如收缩为原来表大小的一半，首先删除这个数据并创建一般大小的新表，将原来散列表中的数据插入新创建的表中，然后把老的表析构。

表收缩时判断的装载因子的选择很重要，如果表扩张选择的两倍大小，而表收缩是选择装载因子为二分之一，这时如果在表扩张后立马删除数据，又反复的插入，删除数据，这样会导致表大小的震荡。这种情况下时间机器浪费时间。
所以我们通常可以选择该装载因子为四分之一来避免这个问题。

无论是表扩张还是表收缩，我们都可以用平摊分析来证明动态表的插入和删除操作的平均代价还是O(1)。详细情况参考书中内容，这里不做赘述。

留言與分享

16. 贪心算法

求解最优化问题的算法通常需要经过一系列的步骤，在每个步骤都面临多种选择。对于许多最优化问题，使用动态规划算法来求最优解有些杀鸡用牛刀了，可以使用更简单、更高效的算法．贪心算法就是这样的算法，它在每一步都做出当时看起来最佳的选择。也就是说，它总是做出局部最优的选择，寄希望这样的选择能导致全局最优解。

活动选择问题

我们的第一个例子是一个调度竞争共享资源的多个活动的问题，目标是选出一个最大的互相兼容的活动集合。假定有一个 n 个活动的集合$S={a_1, a_2, ... , a_n}$，这些活动使用同一个资源（例如一个阶梯教室），而这个资源在某个时刻只能供一个活动使用。每个活动$a_i$都有一个开始时间$s_i$和一个结束时间$f_i$ ，其中$0\le s_i < f_i < \infty$。如果被选中，任务$a_i$发生在半开时间区间$[s_i, f_i)$期间．如果两个活动$a_i$和$a_j$满足$[s_i, f_i)$和$[s_j, f_j)$不重叠，则称它们是兼容的．也就是说，若$s_i\ge f_j$或$s_j\ge f_i$，则$a_i$和$a_j$是兼容的．在活动选择问题中，我们希望选出一个最大兼容活动集。假定活动已按结束时间的单调递增顺序排序：

$f_1 \le f_2 \le f_3 \le ... \le f_{n-1} \le f_n$

例如下面的活动集合S：

对于这个例子，子集$S={a_3, a_9,a_11}$由相互兼容的活动组成。但它不是一个最大集，因为子集$S={a_1, a_4, a_8,a_11}$更大。实际上$S={a_1, a_4, a_8,a_11}$是一个最大兼容活动子集，另一个最大子集是
$S={a_2, a_4, a_9,a_11}$。

最优子结构

假定集合$S_{ij}$（$a_i$结束之后，$a_j$开始之前的活动）的一个最大相互兼容的活动子集为$A_{ij}$，而且$A_{ij}$包含了活动$a_k$。 由于最优解包含了活动$a_k$，我们得到两个子问题：$S_{ik}$（$a_k$开始之前的活动）的兼容活动 和 $S_{kj}$（$a_k$结束之后的活动）的兼容活动。由剪切-粘贴法可以证明$S_{ij}$的最优解为$S_{ik}$的最优解、$a_k$、 $S_{kj}$的最优解组成。即$A_{ij} = A_{ik} \cup a_k \cup A_{kj}$。
所以这时我们可以用动态规划方法求出所有k的取值情况对应的解，然后找出一个最大的作为最优解。
如果用$c[i, j]$表示$S_{ij}$的最优解的大小，递归式为：

$c[i, j] = \left \{ \begin{aligned} & 0 & if \quad S_{ij} = \varnothing, \\ & \max_{a_k \in S_{ij}}\{c[i, k] + c[k, j] + 1\} & if \quad S_{ij} \ne \varnothing, \end{aligned} \right.$

贪心选择

动态规划需要考虑每种子问题，比较之后得出哪种选择是最优解。假如我们无需求解每种子问题，直接就可以找出一个最优选择。那么将大大减少计算过程。对于活动选择问题，我们可以只考虑一个选择：贪心选择。

直观上，我们应该选择一个活动，使得选择它后剩下的资源可以尽可能多的被其他活动利用。直觉告诉我们选择S中最早结束的活动，因为他可以剩下尽可能多的资源。由于我们活动时按照结束时间排序的，也就是说贪心选择就是$a_1$。

当做出贪心选择后，只剩下一个子问题需要求解，因为不会有在$a_1$开始前结束的活动。加上前面的最优子结构性质，所以S的最优解就是$a_1 \bigcup A_{1n}$。

证明贪心选择——最早结束的活动总是最优解的一部分：

定理： 考虑任意非空子问题$S_k$，另$a_m$是$S_k$种最早结束的活动，则$a_m$在$S_k$的某个最大兼容活动子集中。

证明： $A_k$是$S_k$的某个最大兼容活动子集，$a_j$是$A_k$种最早结束的活动。如果$a_j = a_m$，则已经证明$a_m$在$S_k$的某个最大兼容活动子集中；如果$a_j \ne a_m$，那么用$a_m$替换$A_k$中的$a_j$产生$A_k^\prime$，由于$f_m \le f_j$而且$A_k$中的活动都是不相交的，所以$A_k^\prime$也是$S_k$的最大兼容活动子集，得证。

递归贪心算法

为了方便算法初始化，添加一个虚拟活动$a_0$，其结束时间$f_0 = 0$，这样子问题$S_0$就是完整的活动集S。求解原问题即可调用 RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n)。

2,3行是为了找到第一个，与$a_k$不相交的最先结束的活动$a_m$。

迭代贪心算法

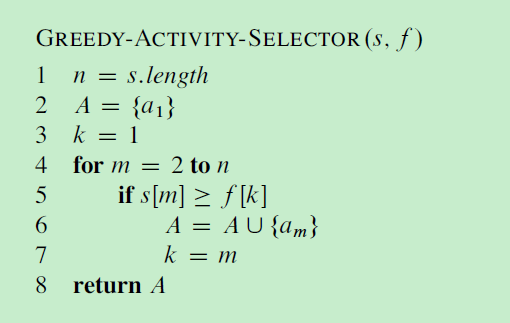
贪心算法原理

前面我们讨论活动选择问题的贪心算法的过程比通常的过程繁琐一些，我们当时经过了如下几个步骤：

1. 确定问题的最优子结构．
2. 设计一个递归算法（动态规划）。
3. 证明如果我们做出一个贪心选择，则只剩下一个子问题。
4. 证明贪心选择总是安全的（步骤 3 、 4 的顺序可以调换）。
5. 设计一个递归算法实现贪心策略。
6. 将递归算法转换为迭代算法。

这个过程详细的看到贪心算法是如何以动态规划为基础的。
更一般地，我们可以简单按如下步骤设计贪心算法：

1. 将最优化问题转化为这样的形式：对其做出一次选择后，只剩下一个子问题需要求解。
2. 证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的。
3. 证明做出贪心选择后，剩余的子问题满足性质：其最优解与贪心选择组合即可得到原问题的最优解，这样就得到了最优子结构。

在本章剩余部分中，我们将使用这种更直接的设计方法．但我们应该知道，在每个贪心算法之下，几乎总有一个更繁琐的动态规划算法。

在证明一个问题可以用贪心算法解决过程中，证明一个问题的贪心选择性质 和 最优子结构性质 是非常重要的。

赫夫曼编码

赫夫曼编码k而已有效的压缩数据：通常可以节省20%~90%的空间，具体压缩率依赖于数据的特型。我们将待压缩数据看做字符序列。根据每个字符出现的频率，赫夫曼贪心算法构造出字符的最优二进制表示。

下面给出一个例子，待压缩文件有10万个字符数据。文件中出现了6种不同的字符，出现的次数见表格：

如果用定长编码来存储信息，那么需要用3位来表示z和6个字符。这种方法总共需要300000个二进制位来存储。
但如果用变长编码来存储信息，如表格中所示，出现频率较高字符的使用短一点的二进制编码表示。这种方法需要$(45 \times 1 + 13 \times 3 + 12 \times 3 + 16 \times 3 + 9 \times 4 + 5 \times 4) \times 1000 = 224000$位。与定长编码相比节约了25%的空间。

我们这里只考虑前缀码，即没有任何码字是其他码字的前缀。只考虑前缀码的原因是，前缀码与任何其他编码方式比都可以保证最优的压缩率，但此处不予证明。
前缀码的作用是简化解码过程，由于没有任何码字是其他码字的前缀，所以文件开头的码字是无歧义的。我们可以简单的识别出开始码字，将其转换为对应的字符，然后对文件剩余部分重复的做这种解码过程。
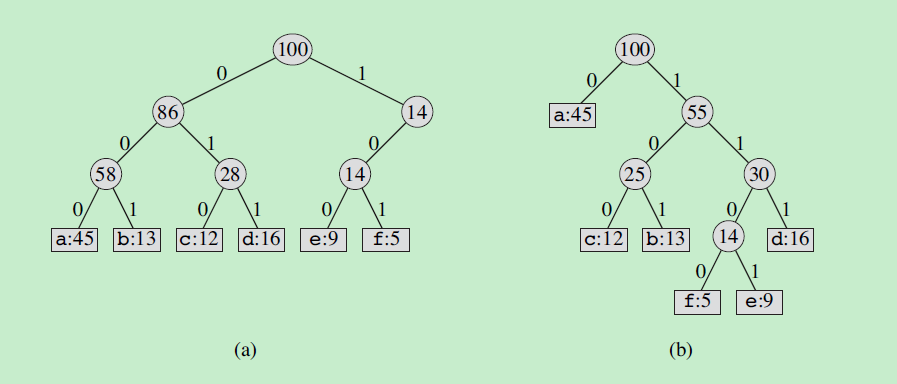
编码方案可以用一个二叉树表示——编码树。下图a表示了定长编码的编码树，图b表示了变长编码的编码树。叶子结点为字符，并存储字符的出现频率，字符的二进制编码是从根节点到叶子节点的路径，向左表示0，向右表示1。内部结点不存储字符，存储子节点的频率和。

给定一棵对应前缀码的树T，我们可以容易地计算出编码一个文件需要多少个二进制位。对于字母表C中的每个字符c，令属性c.freq表示c在文件中出现的频率，令$d_T(c)$表示c的叶结点在树中的深度。注意，$d_T(c)$也是字符c的码字的长度。则编码文件需要习：

$B(T) = \sum_{c \in C}c.freq\cdot d_T(c)$

个二进制位，我们将B(T)定义为T的代价。

构造赫夫曼编码

赫夫曼设计了一个贪心算法得到最优前缀码，被称为赫夫曼编码。

下面是哈夫曼算法的伪代码，输入一个字母表C，输出一个最优前缀码对应的编码树。

构造编码树的过程如下：
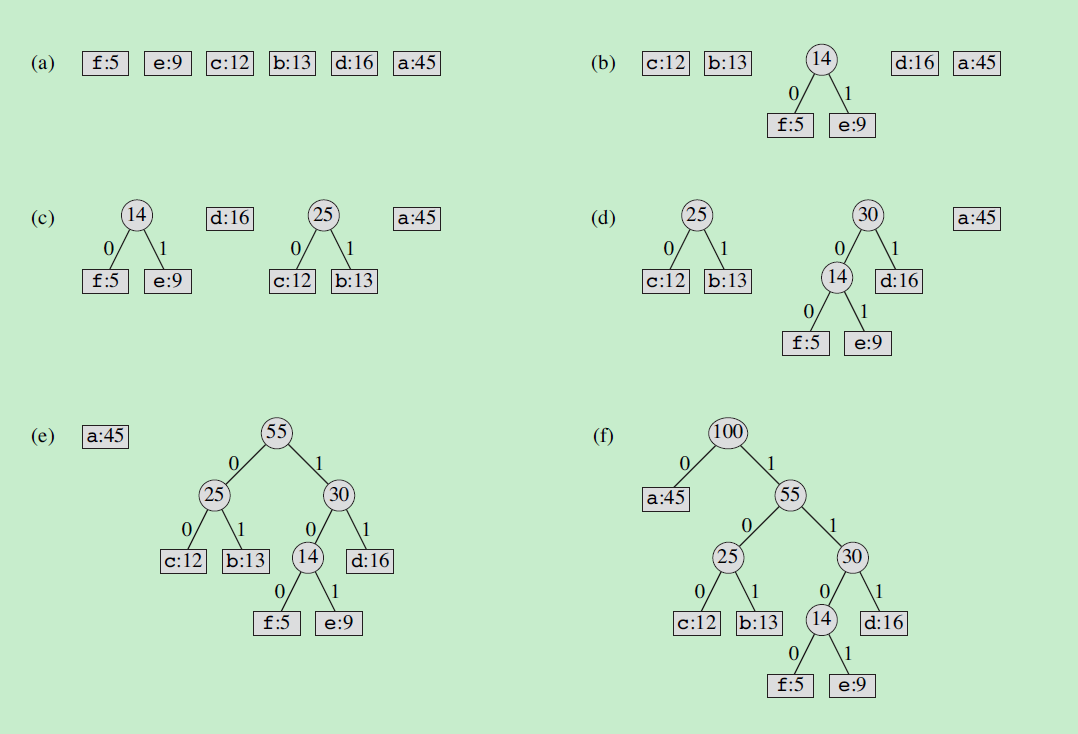
算法中使用一个优先队列Q，初始化时将字母表C全部插入Q。每次循环时，创造一个结点z，从优先队列取出两个最小值作为结点z的孩子，并使得z.freq为两个孩子的freq之和，然后将z结点重新插入优先队列Q中。直到优先队列中只剩下一个元素，这时这个元素为编码树的root结点，并且所有字符都已加入编码树。

下面是一个例子：

证明赫夫曼算法的正确性

贪心选择

贪心选择性质：若x,y是C中频率最低的两个字符。那么C存在一个最优前缀码，x,y的码字长度相等，且只有最后一个二进制位不同。

证明思路，假设有一个最优前缀码的编码树$T$，把x,y与编码树中深度最深的两个兄弟节点进行交换产生$T^\prime$。通过计算得出$B(T^\prime) \le B(T)$。

最优子结构

最优子结构性质：若x,y是C中频率最低的两个字符。令$C^\prime$为$C$去除x和y，然后加入字符z，且$z.freq = x.freq + y.freq$。$T^\prime$为$C^\prime$的一个最优前缀码的编码树，将$T^\prime$中的叶子节点z替换为一个以x,y为子节点的内部节点得到树$T$。则T为C的一个最优前缀码的编码树。

证明思路，反证法，假设C存在一个$T^{\prime\prime}$比T更优，由贪心选择性质可知x,y为兄弟节点（不一定吧？书中用不失一般性，不太理解），将$T^{\prime\prime}$中的x,y替换为z得到$T^{\prime\prime\prime}$，结果得到$B(T^{\prime\prime\prime}) < B(T^{\prime})$，与$T^\prime$为$C^\prime$的一个最优前缀码的编码树的假设相悖。

涉及算法

点击查看实现

• 活动选择问题
• 赫夫曼编码

留言與分享

15. 动态规划

动态规划和分治法相似，都是通过组合子问题的解来求解原问题的解。但不同的是分治法将问题划分为不相交的子问题，递归的求解子问题，再将它们的解组合起来，求出原问题的解。相反，动态规划应用于子问题相互重叠的情况，即不同的子问题具有公共的子子问题。这种情况下，用分治法会反复的求解相同的子问题，造成时间浪费。动态规划对每个子问题只求解一次，并且保存在表格中，从而避免重复计算。

动态规划通常用于求解最优化问题。

我们通常按照如下步骤设计一个动态规划算法：

1. 刻画一个最优解的结构特点
2. 递归的定义最优解的值
3. 计算最优解的值，通常采用自底而上的方法
4. 利用计算出的信息构造一个最优解

如果只需要最优解的值，而非最优解本身，可忽略第四步。如果需要做第四步，往往需要在执行第三步时维护一些额外信息。

钢条切割

钢条切割问题：给定一段长度为n英寸的钢条和一个价格表p_i(i=1,2…n)，求切割方案使得收益r_n最大。

考虑当n=4时，所有的切割方案如下，我们发现当把4英寸的钢条切割为两段2英寸长的钢条时产生的收益最大。

当区分1+3切法和3+1切法时，n英寸的钢条有2^n-1种切割方案。
我们可以手动得到r_i，及对应切割方案：

对于r_n，我们可以用更短的钢条的最优切割收益来描述它：
$r_n = max(p_n, r_1+r_{n-1}, r_2+r_{n-2},...,r_{n-1}+r_1) .$

这时我们找到了钢条切割问题的最优子结构。每次切割后我们可以把切开的两段钢条看做独立的钢条切歌问题。一段钢条的最优解为所有切割方案中最大的。
我们可以将r_n的式子简化为：$r_n=\max\limits_{1\le i\le n}(p_i+i_{n-i})$ .

自顶而下的递归实现

根据上面的式子，我们可以得到下面这种自顶而下的递归实现（p为价格数组）：

这种实现的递归式为：$T(n) = 1 + \sum\limits_{j=0}^{n-1}T(j).$
我们可以求得$T(n) = 2^i$，这个时间是非常惊人的，而这么大的原因就是因为包含了非常多的重复计算。下图是递归树，红线圈起来的都是重复计算部分。

使用动态规划方法

• 带备忘的自顶而下法
  与前面的递归方法类似，但是用了一个数组r[1…n]记录最优解，如果发现r[n]已经有记录，则无需重复计算，直接返回该值。
  
• 自底而上法
  自底而上法采用子问题的自然顺序，依次求解规模为j=1,2…,n的子问题。
  

无论是带备忘的自顶而下法还是自底而上法，其中都是用了一个额外数组来存储子问题的最优解，从而避免重复计算子问题的解。动态规划付出额外的内存空间来节省时间，是典型的时空权衡的例子。

子问题图

当思考动态规划问题时，弄清所涉及子问题及子问题之间的依赖关系很关键。
问题的子问题图准确的表达了这些信息：

途中结点表示钢条切割的子问题规模，箭头表示子问题之间的依赖关系。
有了子问题图，我们便可轻易的得知自底而上的顺序应该如何。
而且子问题图G=(V, E)还可以帮助我们确定动态规划算法的运行时间。由于每个子问题只求解一次，因此算法运行时间等于每个子问题求解时间之和。通常，一个子问题的求解时间与子问题图中对应顶点的度（射出边的数目）成正比，而子问题的数目等于子问题图的顶点数。因此，通常情况下，动态规划算法的运行时间与顶点和边数量呈线性关系。

重构解

前面的方法只给出的如何求出最优解的值，但并未返回解本身。
下面是基于自底而上动态规划算法的扩展，其中用数组s[0…n]存储n英寸钢条的最优切割方案，s[i]存储的数字表示，i英寸的钢条切割为s[i]英寸和i-s[i]英寸时最优，其中s[i]英寸部分不再切割，i-s[i]英寸部分的最优解需要递归查看。
所以可以通过PRINT-CUT-ROD-SOLUTION来打印出n英寸钢条的一个最优切割方案。

矩阵链乘法

给定一个n个矩阵的序列（矩阵链）$<A_1, A_2, ..., A_n>$，我们希望求他们的乘积$A_1A_2...A_n$，由矩阵乘法的结合律我们可知给乘积链随意的加上括号不会改变最终的结果，但是不同的括号会影响矩阵链乘法的时间。
以矩阵链$<A_1, A_2, A_3>$为例，三个矩阵的规模分别是10×100、100×5和5×50。如果按照$((A_1A_2)A_3)$的顺序计算，$A_1A_2$（规模10×5）需要做10×100×5=5000次标量乘法，再与$A_3$相乘又需要10×5×50=2500次标量乘法，总共需要7500次标量乘法。如果按照$(A_1(A_2A_3))$的顺序计算，$A_2A_3$（规模100×50）需要做100×5×50=25000次标量乘法，A₁再与之相乘又需要10×100×50=50000次标量乘法，总共需要75000次标量乘法。因此，按照$((A_1A_2)A_3)$的顺序比按照$(A_1(A_2A_3))$的顺序快了10倍。
所以引入了矩阵链乘法问题：给定n个矩阵的链$<A_1, A_2, ..., A_n>$，矩阵i的规模为$p_{i-1} \times p_i$，求一个完全括号化方案，使得计算乘积$A_1A_2...A_n$所需的标量乘法次数最少。

我们可以用下面这个递归式表示矩阵链完全括号化方案的个数，这个递归式的解为$\Theta(2^n)$，所以穷举法是不可行的。

$P(n) = \left \{ \begin{aligned} & 1 & if \quad n = 1, \\ & \sum_{k=1}^{n-1}P(k)P(n-k) & if \quad n \ge 2, \end{aligned} \right.$

动态规划法

1. 刻画一个最优解的结构特点
   用$A_{i..j}$表示$A_iA_{i+1}...A_j$。我们可以将$A_{i..j}$分解为子问题$A_{i..k}$和$A_{k+1..j}$，即$A_iA_{i+1}...A_j -> (A_iA_{i+1}...A_k)(A_{k+1}A_{k+2}...A_j)$。然后在对子问题递归求解。
2. 递归的定义最优解的值
   用$m[i,j]$表示$A_{i..j}$所需标量乘法次数的最优值。假设$A_{i..j}$的最优分割点为$k(i<=k<j)$，那么$m[i,j] = m[i,k] + m[k+1,j] + p_{i-1} p_{k} p_{j}$，然而这个分割点我们是不知道的，但是肯定在i和j之间，我们只需找到所有可能中的最小值，所以我们有如下递归式：

$m[i,j] = \left\{ \begin{aligned} & 0 & if \quad i = j, \\ & \min_{i\le k\le j}\{m[i,k] + m[k+1, j] + p_{i-1}p_kp_j\} & if \quad i < j, \end{aligned} \right.$

3. 计算最优解的值，通常采用自底而上的方法
   从上面的递归式能推测出自底而上法的顺序，或者使用子问题图辅助。可以从链长为2的子问题开始求解，一直递增到链长为n的子问题，Done。伪代码如下：
   
   使用m[i,j]存储A_i…j的最优解的值，s[i,j]存储A_i…j的最优分割点k。
   
4. 利用计算出的信息构造一个最优解
   利用s数组存储的最优分割点，我们可以递归的构造出一个最优解，伪代码如下：
   

动态规划原理

虽然已经介绍了两个动态规划问题，但可能还会疑惑到底什么样的问题可以使用动态规划方法解决？
适合用动态规划的最优化问题应该具备两个要素：最优子结构和子问题重叠

最优子结构

动态规划法的第一步便是刻画最优解的结构。如果一个问题的最优解包括子问题的最优解，我们称此问题具有最优子结构性质。
发掘最优子结构性质的过程遵循如下通用模式：

1. 证明问题最优解的第一个组成部分是做出一个选择
2. 对于一个给定问题，假定已经知道哪种选择会得到最优解
3. 给定可获得最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好的刻画子问题空间
4. 利用“剪切-粘贴”技术证明：作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。

   利用反证法：假设子问题的解不是其最优解，那么我们可以“剪切”掉这个非最优解，将最优解“粘贴”进去，从而得到一个更优的解，这与最初的解是原问题最优解的前提假设矛盾。

对于不同问题领域，最优子结构的不同体现在：

1. 原问题的最优解涉及多少个子问题（一个问题分解为多少个子问题）
2. 在确定最优解使用那些子问题时，我们需要考虑多少种选择（有多少种分解方式）

重叠子问题

如果递归算法反复求解相同的子问题，我们就称最优化问题具有重叠子问题性质。与之相对的，适合用分治法求解的问题通常在递归的每一步都生成全新的子问题。
动态规划通常这样利用重叠子问题的性质：对每个子问题只求解一次，将解存入一个表中，当再次需要这个子问题时直接查表，查表的代价为常数时间。

最长公共子序列

一个给定序列的子序列是降给定序列中零个或者多个元素去掉后的结果。
给定两个序列X和Y，如果Z既是X的子序列，又是Y的子序列，那么Z为X和Y的公共子序列。
最长公共子序列问题给定两个序列X={x₁, x₂, …, x_m}和Y={y₁, y₂, …, y_n}，求X和Y长度最长的公共子序列。

1. 刻画一个最优解的结构特点
   
2. 递归的定义最优解的值

$c[i,j] = \left\{ \begin{aligned} & 0 & & if \quad i = 0 \quad or \quad j = 0, \\ & c[i-1,j-1]+1 & & if \quad i,j > 0 \quad and \quad x_i = y_j, \\ & max(c[i,j-1], c[i-1, j]) & & if \quad i,j > 0 \quad and \quad x_i \neq y_j, \end{aligned} \right.$

3. 计算最优解的值，通常采用自底而上的方法
   
   c[i, j] 存储序列X_1->i和Y_1->j最长公共子序列的长度
   b[i, j] 存储序列X_1->i和Y_1->j最优解依赖的子问题的方向
4. 利用计算出的信息构造一个最优解
   
   当b[i, j]存储的是“↖”时，表示x_i和y_j相同。
   所以从b[m, i]开始，训着箭头方向查找“↖”，便可以找到一个最长公共子序列。
   伪代码如下：
   

涉及算法

点击查看实现

• 钢条切割
• 矩阵链乘法
• 最长公共子序列

留言與分享

14. 数据结构的扩张

一些工程应用需要的只是教科书中的标准数据结构，也有许多其他的应用需要对现有数据结构进行少许的创新和改造，但只有很少的情况需要创造全新类型的数据结构。
更经常的是，通过存储额外信息的方法来扩张标准的数据结构，然后对这种数据结构编写新的操作来支持所需要的应用。

比如：

动态顺序统计量

之前我们讨论了中位数和顺序统计量，对于一个无序的集合，我们可以在$\Omicron(n)$的时间内确认任何顺序统计量。这里我们将介绍如何修改红黑树，使得可以在$\Omicron(\lg n)$时间内确认任何的顺序统计量。以及如何在O(lgn)时间内得到一个元素的秩，即它在集合线性序中的位置。

下图展示了一种支持快速顺序统计的数据结构，顺序统计树。这种数据结构是在红黑树的基础上，给每个元素添加一个属性size。一个结点的size表示以这个结点为根结点的子树大小。我们定义哨兵T.nil的size为0，则有如下等式

x.size = x.left.size + x.right.size + 1

查看给定秩的元素

从根结点开始查找，首先通过左孩子的size+1得到当前结点为根节点时的秩r，然后和需要查找的秩i作比较。如果相等则直接返回，如果i < r 查看左孩子，否则递归查看右孩子，但是查看右孩子时，需要传入i - r，因为右子树并不能知道左子树的大小，而右孩子实际的轶为r+右孩子为根结点时的右孩子的秩：

RANK(x.right) = RANK(x) + (x.right.left.size + 1)

查看一个元素的秩

假如一个元素x的父结点为根结点，
当这个元素x是根结点的左孩子时，$RANK(x) = x.left.size + 1$
当这个元素x是根结点的右孩子时，$RANK(x) = RANK(x.p) + x.left.size + 1$

利用上面的性质，求解一个元素x的秩时，我们循环的求解当x的父结点为根结点时，x在这个子树中的大小，每次循环上移一层，直到移动到真实的root结点，这时我们已经求出了该元素真实的秩。

维护size

当插入/删除元素时，除了维护红黑树的特性，我们还要维护结点的size属性。正常的插入/删除导致的size变化比较简单，不在赘述。我们看看当发生旋转时size的维护：

当对x做左旋后，我们需要重新计算x的size，并且把x之前的size赋给y，因为旋转不会影响这个局部子树的size。
当对y做右旋后，我们需要重新计算y的size，同理把y之前的size赋给x。

如何扩张数据结构

扩张一种数据结构可以分为4个步骤：

1. 选择一种基础数据结构
2. 确定基础数据结构中要维护的附加信息
3. 检验基础数据结构上的基本修改操作能否维护附加信息
4. 设计一些新操作

在扩张数据结构时，不一定非得时上述结构，上述只是一个一般模式。但我们可以把上述步骤作为一个check list来检验扩张数据结构是否完善。

区间树

有些问题可能会涉及到区间数据，这时候可能就需要用到区间树。比如：查看某一时间段内发生的事。

我们把一个区间[l, h]表示成一个对象i，i.low = l为低端点，i.high = h为高端点。
下图展示了两个区间的三种状态：

• a，区间i和区间i’重叠
• b，区间i在区间i’的左边（i.h < i’.l）
• c，区间i在区间i’的右边（i.l > i’.h）

区间树是一种对红黑树扩展的数据结构，我们看看红黑树扩展为区间树的过程：

1. 基础数据结构
   选择红黑树，每个元素包含区间属性x.int，x的key为x.int.low。
2. 附加信息
   每个结点除了区间信息外，包含一个值x.max，它表示以x为根结点子树中所有端点的最大值。
3. 对信息的维护
   在插入/删除操作后，需要对max值做维护，最多影响树高h个元素的max值，而且每次维护只需要常数次操作。所以不会影响原有操作的时间复杂度。

   x.max = max(x.int.high, x.left.max, x.right.max)

4. 设计新的操作
   新操作INTERVAL-SEARCH(T, i)，用来查找区间树T中与区间i重叠的结点。若树中没有区间与i重叠，则返回T.nil。

INTERVAL-SEARCH(T, i)：将x指向root结点开始循环查看x是否与i重叠，如果重叠则退出循环返回x。如果x有左孩子且左孩子的max值大于等于i.low，则循环查看x的左孩子，否则循环查看x的右结点。

TODO: 用循环不变式证明各个扩张的正确性

留言與分享

13. 红黑树

二叉搜索树的各种操作时间复杂度为$\Omicron(h)$，但是树的高度h不可控，最差的情况为n。
而平衡搜索树能将树的高度控制在$\Omicron(\lg(n))$。
常见的平衡搜索树有：

• AVL树
• 红黑树
• treap （tree + heap，给每个元素随机的priority，从而间接的实现随机插入，使得树的期望高度为$\Omicron(\lg(n))$）
• B树 （十八章介绍）
  • 2-3-4树

本章重点讨论红黑树，以及习题中出现的AVL树。AVL树较为简单所以先介绍AVL树。

AVL树

AVL树由Adel’son-Vel’skii & Landis 在1962年发明，由他们的名字命名。
比较一般的二叉搜索树，每个结点额外存储它的高度，nil的高度为0，其他节点的高度为Height(x) = max(Height(x->left), Height(x->right)) + 1。每个结点两个孩子的高度差不能超过1。
当右子树的高度比左子树的高度高时，我们称right-heavy（如下图），反之这称left-heavy。

AVL树的各种查询操作都和普通二叉搜索树无异，所以我们只需关注会改变树结构的Insert操作和Delete操作。
在一般的Insert或者Delete操作后，结点的高度会变，所以有可能会违反AVL树的性质，这时候我们需要引入一个操作Rotate（旋转）

Rotate

旋转分为两种，左旋（LEFT-ROTATE）和右旋（RIGHT-ROTATE）。下图右测变为左侧的情况称为对x结点左旋，左侧变为右侧的情况称为对y结点做右旋。

我们可以发现旋转操作并不会影响二叉搜索树的性质。
旋转前后都会保持α <= x <= β <= y <= γ
下面是左旋的伪代码，右旋的操作和左旋对称，不再赘述。

Ref：AVLTree::LeftRotate & AVLTree::RightRotate in AVLTree.h

AVL树平衡调整（ADJUST_FROM(x)）

当Insert或者Delete一个元素后，平衡有可能被破坏，假设x是最底层被破坏性质的节点，而且是right-heavy时（left-heavy是对称的）：

1. Balance
   • 如果x的右孩子y是平衡的或者right-heavy的（Figure 5）
     • 我们对x做LEFT-ROTATE操作可使其恢复平衡
     • 然后重新计算x和y的高度
   • 如果x的右孩子z是left-heavy的（Figure 6）
     • 我们先对z做RIGHT_ROTATE，然后对x做LEFT-ROTATE，可使其恢复平衡
     • 然后重新计算x，y，z的高度
2. Loop
   • 重新计算x的高度，并使得x=x->p继续循环，直到根节点
   • 若图中发现某节点不平衡的用1. Balance

Ref：AVLTree::AdjustFrom in AVLTree.h

AVL树 Insert

因为插入的节点肯定是叶子节点，所以直接对插入节点调用ADJUST_FROM(x)即可。

Ref：AVLTree::Insert in AVLTree.h

AVL树 Delete

删除操作略为复杂，可能会影响子节点的平衡。

• 当被删除节点只有一个孩子，或者没有孩子时，被删除节点的孩子不会被应用
  • 这时对删除节点原来的父节点调用ADJUST_FROM(x)即可
• 当被删除节点有两个孩子时
  • 如果被删除节点右子树的最小节点min的父节点为被删除节点，这时对min调用ADJUST_FROM(x)
  • 其他情况，对min原来的父节点调用ADJUST_FROM(x)

Ref：AVLTree::Delete in AVLTree.h

红黑树

红黑树也是一种平衡二叉树。它在每个节点上增加一个存储位color来表示节点的颜色，节点的颜色为RED或者BLACK。通过对任何一条从根节点到叶子节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出2倍，所以是近似于平衡的。
红黑树还定义一种NIL节点，NIL节点是红黑树的叶子结点（外部节点），真实的数据组成树的内部节点（如下图a所示）。
红黑树的具体性质如下：

1. 每个节点不是红色的就是黑色的
2. 根节点是黑色的
3. 每个叶结点（NIL）是黑色的
4. 如果一个结点是红色的，那么它的两个孩子都是黑色的
5. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，黑色结点的数量相同

为了方便处理，使用一个哨兵来替代NIL结点。对于一颗红黑树T，哨兵T.nil是一个普通结点。它的color为BLACK，用哨兵T.nil替换图a中的所有NIL，这样就形如下图b所示，T.nil的p, left, right, key属性我们并不关心，所以方便起见程序中可以对其值随意设定。

为了方便起见，我们在图中省去T.nil，这样就变成了图c的样子。

NULL -> T.nil

红黑树与普通二叉搜索树相比，用T.nil替代了空指针。
所以所有操作中用到空指针的地方，需要换成T.nil。后面不做赘述。

红黑树 Insert

红黑树的插入操作，除了一般的操作外，还需要把插入结点的颜色设为RED。因为插入了一个红色的结点，所以有可能触犯红黑树的一些性质（1,4），所以我们要调用RB-INSERT-FIXUP将其修正。

RB-INSERT-FIXUP会循环的查看z的父结点是否违反性质4，如果违反，则将其修正。如果修正后仍然有可能违反性质4，则继续循环查看其爷结点。（本文只讨论插入结点的父结点为爷结点的左孩子的情况，右孩子的情况与其对称，不再赘述。）

修正过程有三种情况：

• Case 1. z的叔结点为红色
• Case 2. z的叔结点为黑色，且z是父亲的右孩子
• Case 3. z的叔结点为黑色，且z是父亲的左孩子
  

上图插入4之后的处理过程。下面我们详细讨论下三种情况的处理方式：

• Case 1
  这种情况只需改变着色，将父节点和叔结点染成黑色，爷结点染成红色。
  因为爷结点以前是黑色，却染成了红色，如果爷结点的父结点为红色，这时仍会触犯性质4，所以我们将爷结点赋给z，下次循环时再修正它。
  如果z的爷结点为root结点，我们修正后root结点变成了红色，并且让z指向root结点然后跳出了循环。在循环外边我们会将z重新染成黑色，所以保持了性质1。
  

• Case 2/3
  当z是父结点的左孩子时，符合Case 3，这时我们只需把爷结点做右旋，然后交换之前父结点和爷结点的颜色。这时局部的根节点颜色没有改变，仍然是黑色，所以整个树都满足了红黑树的特性，无需继续循环。
  
  当z是父结点的右孩子时，符合Case 2，这时只需要对父结点做左旋，使其变为Case 3的情况。

由上可知，一旦循环进入Case 2或者Case 3，就会结束循环。所以一次插入操作最多只会有两次旋转操作。尽量少的循环操作是非常有益的，因为改变结点颜色并不会影响查找功能，当多线程处理时我们只需给旋转操作加锁。

红黑树 Delete

删除操作比插入操作略微复杂，当删除一个黑色结点，或者删除过程中移动了一个黑色结点时，都有可能破坏红黑树的性质（2,4,5）。

当被删除的结点只有一个孩子，或者没有孩子，这时我们只需关心被删除结点的颜色，如果被删除的结点为红色，则无需修正，如果被删除结点为黑色，则需要从被删除结点的孩子开始修正。

当被删除的结点有两个孩子时，我们会找右子树的最小结点来替代被删除结点的位置和颜色，所以这是我们需要关注这个最小结点的颜色，如果最小结点的颜色为红色，则无需修整，如果这个最小结点为黑色，则需要从最小结点的右孩子开始修正。

从x开始修正时，有五种情况：

• Case 0. x为红色
  • 这时23行会将其设为黑色，可直接满足所有红黑树性质
• Case 1. x的兄弟结点w为红色
• Case 2. x的兄弟节点w为黑色，且w的两个孩子都是黑色
• Case 3. x的兄弟节点w为黑色，且w的右孩子为黑色，左孩子有红色
• Case 4. x的兄弟节点w为黑色，且w的右孩子为红色

• Case 1
  这种情况我们将其转换为Case2/3/4

  1. 设置兄弟节点w为黑色，父结点为红色
  2. 左旋父结点
  3. 重新设置w为x的兄弟结点

• Case 2
  这种情况将兄弟结点w设置为红色，并且x=x.p，继续循环。
  我们会发现，如果是从Case 1转换到Case 2，那么x.p一定是红色，所以会直接退出循环。

• Case 3
  这种情况我们将其转换为Case4

  1. 设置兄弟节点w为红色，w的左孩子为黑色
  2. 右旋w结点
  3. 重新设置w为x的兄弟结点

• Case 4
  这种情况可以做一些修改，然后结束修正

  1. 设置w的颜色为x父结点的颜色
  2. x父结点的颜色设置为黑色
  3. w右孩子的颜色设置为黑色
  4. 左旋x的父结点
  5. 使x指向root结点，从而结束修正

由上可知，一旦循环进入Case 1, Case 3，Case 4，就会结束循环。所以一次插入操作最多只会有三次旋转操作（Case 1 -> Case 3 -> Case 4）。

性质维护:

插入过程中维护性质的分析：

1
2

Case1 转换后，局部的黑高与之前相同
但是由于将局部根节点C从黑色变成红色，所以需要继续考虑C是否违反性质4

1
2

Case2/3 转换后，局部的黑高与之前相同
并且局部根节点B的颜色没有改变，所以直接Done

删除过程中维护性质的分析：

需要修正时，被修正结点x以前的父节点肯定为黑色，x替代了x以前父节点的位置
所以这时这个子树（x为根节点）的黑高减少了1

1
2
3
4

Case1 转换后，ABCDE的黑高都没有变
所以这时仍然是x为根节点的子树黑高少1

根本情况没有变化，变化的只是x的兄弟节点的颜色

1
2
3
4
5

Case2 转换后，以x的父节点c为根节点的子树已经满足红黑树的性质
但是c为根节点的子树的黑高比之前少1

所以令c为新的x，继续调整

1
2
3
4
5

Case3 转换后，ABCDE的黑高都没有变
所以这时仍然是x为根节点的子树黑高少1

根本情况没有变化，变化的只是w的右孩子的颜色

1
2
3
4
5

Case4 转换后，以c为根节点子树满足红黑树性质
并且根节点的颜色没有变化，子树的黑高也没有变化

所以Done

涉及数据结构

点击查看实现

• AVL树
• 红黑树

留言與分享

12. 二叉搜索树

二叉搜索树支持许多动态集合的操作，包括Search，Insert，Delete，Minimum，Maximum，Successor，Predecessor。所有操作的时间复杂度为$\Omicron(h)$，h为树的高度。

二叉搜索树

二叉搜索树是一个链式存储的二叉树，且具有如下特性：
设x为二叉搜索树中的一个结点。

• 如果y是x左子树中的一个结点，那么y.key<=x.key。
• 如果y是x右子树中的一个结点，那么y.key>=x.key。

Search

从根节点开始查找，如果查询的k小于根节点的key，则递归查找左子树；如果查询的k大于根节点的key，则递归查找右子树；如果查询的k等于根节点的key，done。

Minimum

从根节点开始沿着left child方向一直找到低。

Maximum

从根节点开始沿着right child方向一直找到低。

Successor & Predecessor

查询x的下一个节点：

• 如果x有右孩子，那么x的下一个节点就是右子树的最小值。

  1 2 3 4 5 6 7

  ○ / \ ● / \ ○ / \ [○]

• 若果x没有右孩子，那么x的下一个节点是x的第n个parent，这个parent是第一个符合下图的情况，第n-1个parent 是第n个parent得 left child。

  1 2 3 4 5 6

  [○] / \ ○ / \ ● /

• 如果没有符合这样情况的parent，那么说明x是最大数，没有下一个节点。

Insert

上图描述了插入key为13的数据。
从根节点x开始查找。如果待插入数据小于该节点数据，到左子树继续查找，否则到右子树查找，直到找到一个空位置，将数据放入。

Delete

删除操作的情况较为复杂，有如下几种情况

1. 待删除节点没有孩子
2. 待删除节点只有一个孩子，如下图(a) (b)情况
3. 待删除节点有两个孩子，并且右孩子没有左孩子时，如下图©情况
4. 待删除节点有两个孩子，并且右孩子有左孩子时，如下图(d)情况

1. 当待删除节点没有孩子时：
   • 可以直接删除该节点，并且修改他的父节点，用nil代替他
2. 当待删除节点只有一个孩子时，如图中 (a) (b) 情况：
   • 可以直接用子节点替换该节点
3. 当待删除节点有两个孩子时，如图中 © (d) 情况：
   • 思路：用待删除节点z的Successor节点y替代它的位置
   • 情况c，右孩子没有左孩子（y是z的子节点）
     • y替换z，并且接管z的左孩子
   • 情况d，右孩子有左孩子
     • y的右孩子x替换y，并且y接管z的右孩子
     • y替换z，并且接管z的左孩子

Tips：当待删除节点有两个孩子时，用待删除节点的Predecessor节点替代它也可以。

涉及数据结构

点击查看实现

• 二叉搜索树

留言與分享

11. 散列表（哈希表）

许多应用都需要一种动态集合，至少支持Insert，Search和Delete的字典操作。
散列表（Hash Table）是实现字典操作的一种有效数据结构。尽管最坏情况下散列表查询一个元素的时间和链表的查询时间相同，为Θ(n)。但是在实际应用中，散列表的查询性能是极好的。在一些合理的假设下，散列表中扎寻一个元素的平均时间能为Ο(1)。

假设某应用需要用到一个动态集合，其中每个元素的KEY都是取自全域U={0, 1, …, m-1}。本章讨论方法都是基于这样的动态集合。

直接寻址表

当KEY的全域U较小时，直接寻址表是一种简单而有效的技术。
为了表示这个动态集合，我们用一个数组作为直接寻址表，记为T[0…m-1]，其中数组的每个位置称为槽，与全域U中的KEY一一对应。
K集合表示实际存在的元素的KEY集合。
槽k指向KEY为k的元素，如果K集合中没有k，那么T[k] = nil。

散列表

直接寻址表的缺点很明显：

1. 如果全域U非常大，则计算机无法存储
2. 如果K集合相对于全域U非常小，那么将非常浪费空间

如果直接寻址表占用的存储空间为$\Theta(|U|)$，那么散列表能将存储需求降至$\Theta(|K|)$，同时散列表中查找一个元素的时间为$\Omicron(1)$，不过是平均时间。

散列方式不同于直接寻址表的地方是，元素存储在散列表中的位置由散列函数决定，即k元素存储在散列表的h(k)位置。h(k)叫做k的散列值。

散列表T的大小比|U|小很多，所以肯定会有冲突的情况。

冲突最简单的解决方式是使用链接法，后面还介绍一种开放寻址法。
下图是链接法的图示，当有两个k值映射到了同一个散列值时，将它们保存在一个链表内。

链接法散列分析

如果要将n个数据存储在m大小的散列表中，我们称α = n/m为装载因子，即散列表的每个槽平均存放的数据。
假设散列函数能等可能的把数据散列到m个槽中，我们称这个假设为简单均匀散列。
这时每个槽存放元素个数的期望值为α。

所以，一次不成功查找的平均时间为$\Theta(1+\alpha)$。（1 表示散列函数消耗的时间）

1

因为每个槽的期望为α，而不成功的情况下，查找的期望时间就是从槽链表的头遍历到链表尾，所以期望时间就是槽链表的长度α。

一次成功查找的平均时间为$\Theta(1+\alpha)$。

1
2

具体证明参考公开课中老师的推理，或者书中推理。
自我理解：一个元素在槽中的位置是等概率随机的(1/α)，而且期望时间为元素在槽中位置的期望。期望位置为(1+2+..+α)*(1/α) = (α+1)/2

散列函数

最好的散列函数便是能达到简单均匀散列。
下面介绍一些的散列函数。其中全域散列能够达到这样的要求。

除法散列

1

h(k) = k mod m

m最好是一个素数，并且不能太接近2或者10的乘方。

乘法散列

1

h(k) = [(a * k) mod 2^w] >> (w − r)

k是w bits的数
m = 2^r
a最好是一个奇数，并且不能太接近2或者10的乘方。

全域散列

随机的选择散列函数，称为全域散列
Example：

1
2

h(k) = [(ak+b) mod p] mod m 
where a and b are random ∈ {0, 1, . . . p−1}, and p is a large prime (> |U|).

证明全域散列为简单均匀散列的过程，参考公开课中老师的推理，或者书中推理。

开放寻址法

• 无链表，所有的元素都保存在table中
• 每个槽存储一个元素，m>=n
• 散列函数为h(k, i)，i从0开始，当有冲突后i++，直到找到一个空的位置，所以散列函数需要有如下性质：

1
2
3
4
5

对同一个KEY做m次探查，能把散列表填满

h : U × {0, 1,...,m − 1} → {0, 1,...,m − 1}

{h(k, 0), h(k, 1), . . . , h(k, m − 1)} == {0, 1,...,m − 1}

删除时，不能直接删除！删除后需要标记此位为删除位。

线性探查

1

h(k, i) = (h1(k) +i) mod m

双重探查

1
2
3
4

h(k, i) =(h1(k) + i·h2(k)) mod m

h2(k) 需要和 m 互为质数
e.g. m = 2^r, h2(k) 永远为奇数

开放寻址法分析

给定一个装载因子α = n/m < 1的开放寻址散列表，并假设是均匀散列的：
对于一次不成功的查找，期望的探查次数至多为1/(1-α)
对于一次成功的查找，期望的探查次数至多为\frac{1}{α}\ln(1/(1-α))

完全散列

基于全域散列，完全没看。。。

涉及数据结构

点击查看实现

• 使用链接法的散列表

留言與分享

10. 基本数据结构

动态集合的基本数据结构。

栈

栈，后进先出，用数组存储，并用top保存栈顶位置。支持压入（Push）和弹出（Pop）操作。
a->b产生了两次Push操作，压入了17和3。
b->c产生了一次Pop操作，弹出了3。

队列

队列，先进先出，用数组存储，用head和tail保存队列的头和尾的位置。支持入队（Enqueue）和出队（Dequeue）操作。
a->b产生了三次Enqueue操作，加入了17 3 5。
b->c产生了一次Dequeue操作，去除了15。
当head或者tail超出数组范围时，转移到数组头部。
当tail等于head时，表示队列已满，不能再加入数据。

链表

链表是一种对象按照线性排序的数据结构，不同于数组的是链表的顺序由各个对象里的指针表示。
下图表示一个双向链表。每个对象包含prev指针，next指针，key值，或者附加一些卫星数据。
prev指针指向上一个对象
next指针指向下一个对象
用一个head指针指向头结点，头结点的prev指针为null
尾结点的next指针为null

单向链表为双向链表去除prev指针。

下图是一个带有哨兵的双向循环链表，说实话没看出这个哨兵的必要性。

数组存储链表

不是所有的语言都支持指针，所以只能间接实现链表。
下图给出一种用多个数组存储链表的方式，next数组和prev数组中存储next元素或prev元素的数组下标，从而间接的实现了双向链表。

为了更方便快捷的在分配和释放数组中的元素，在数组中存储一个free单向连边。
当需要分配元素时，分配free链表的头结点，并使free指向下一元素。
当需要释放元素时，使该元素的next指向free指向的元素，并使得free指向该元素。

二叉树

前面我们讨论过一种特殊二叉树——堆的存储，我们将堆存储在数组中。
但对于一般的二叉树，我们将用链式数据结构表示。

每个元素包含三个指针——p、left、right分别指向父节点、左孩子、右孩子。
根节点的p指向null，叶子节点的left和right指向null。

当我们需要存储一个N叉树时，按照上面的方法，每个元素则需要child1、child2…childN来存储，会占用很多额外空间，如果孩子个数是未知的这种方式则无法实现。
下图展示了一种分支无限制的有限树的存储方式——左孩子右兄弟表示法。left指向第一个孩子，right指向兄弟节点。

涉及数据结构

点击查看实现

• 双向链表

留言與分享