mysql基础教程

2015 年 10 月 12 日分類 database, mysql

为什么需要数据库？

因为应用程序需要保存用户的数据，比如Word需要把用户文档保存起来，以便下次继续编辑或者拷贝到另一台电脑。

要保存用户的数据，一个最简单的方法是把用户数据写入文件。例如，要保存一个班级所有学生的信息，可以向文件中写入一个CSV文件：

id,name,gender,score
1,小明,M,90
2,小红,F,95
3,小军,M,88
4,小丽,F,88

如果要保存学校所有班级的信息，可以写入另一个CSV文件。

但是，随着应用程序的功能越来越复杂，数据量越来越大，如何管理这些数据就成了大问题：

读写文件并解析出数据需要大量重复代码；
从成千上万的数据中快速查询出指定数据需要复杂的逻辑。

如果每个应用程序都各自写自己的读写数据的代码，一方面效率低，容易出错，另一方面，每个应用程序访问数据的接口都不相同，数据难以复用。

所以，数据库作为一种专门管理数据的软件就出现了。应用程序不需要自己管理数据，而是通过数据库软件提供的接口来读写数据。至于数据本身如何存储到文件，那是数据库软件的事情，应用程序自己并不关心：

┌───────────┐
│application│
└───────────┘
     ▲ │
     │ │
 read│ │write
     │ │
     │ ▼
┌───────────┐
│ database  │
└───────────┘

这样一来，编写应用程序的时候，数据读写的功能就被大大地简化了。

数据模型

数据库按照数据结构来组织、存储和管理数据，实际上，数据库一共有三种模型：

层次模型
网状模型
关系模型

层次模型就是以“上下级”的层次关系来组织数据的一种方式，层次模型的数据结构看起来就像一颗树：

            ┌─────┐
            │     │
            └─────┘
               │
       ┌───────┴───────┐
       │               │
    ┌─────┐         ┌─────┐
    │     │         │     │
    └─────┘         └─────┘
       │               │
   ┌───┴───┐       ┌───┴───┐
   │       │       │       │
┌─────┐ ┌─────┐ ┌─────┐ ┌─────┐
│     │ │     │ │     │ │     │
└─────┘ └─────┘ └─────┘ └─────┘

网状模型把每个数据节点和其他很多节点都连接起来，它的数据结构看起来就像很多城市之间的路网：

     ┌─────┐      ┌─────┐
   ┌─│     │──────│     │──┐
   │ └─────┘      └─────┘  │
   │    │            │     │
   │    └──────┬─────┘     │
   │           │           │
┌─────┐     ┌─────┐     ┌─────┐
│     │─────│     │─────│     │
└─────┘     └─────┘     └─────┘
   │           │           │
   │     ┌─────┴─────┐     │
   │     │           │     │
   │  ┌─────┐     ┌─────┐  │
   └──│     │─────│     │──┘
      └─────┘     └─────┘

关系模型把数据看作是一个二维表格，任何数据都可以通过行号+列号来唯一确定，它的数据模型看起来就是一个Excel表：

┌─────┬─────┬─────┬─────┬─────┐
│     │     │     │     │     │
├─────┼─────┼─────┼─────┼─────┤
│     │     │     │     │     │
├─────┼─────┼─────┼─────┼─────┤
│     │     │     │     │     │
├─────┼─────┼─────┼─────┼─────┤
│     │     │     │     │     │
└─────┴─────┴─────┴─────┴─────┘

随着时间的推移和市场竞争，最终，基于关系模型的关系数据库获得了绝对市场份额。

为什么关系数据库获得了最广泛的应用？

因为相比层次模型和网状模型，关系模型理解和使用起来最简单。

关系数据库的关系模型是基于数学理论建立的。我们把域（Domain）定义为一组具有相同数据类型的值的集合，给定一组域D1,D2,…,Dn，它们的笛卡尔集定义为D1×D2×……×Dn={(d1,d2,…,dn)|di∈Di,i=1,2,…,n}，而D1×D2×……×Dn的子集叫作在域D1,D2,…,Dn上的关系，表示为R(D1,D2,…,Dn)，这里的R表示#%&^@!&$#;!~％¥%……算了，根本讲不明白，大家也不用理解。

基于数学理论的关系模型虽然讲起来挺复杂，但是，基于日常生活的关系模型却十分容易理解。我们以学校班级为例，一个班级的学生就可以用一个表格存起来，并且定义如下：

ID	姓名	班级ID	性别	年龄
1	小明	201	M	9
2	小红	202	F	8
3	小军	202	M	8
4	小白	201	F	9

其中，班级ID对应着另一个班级表：

ID	名称	班主任
201	二年级一班	王老师
202	二年级二班	李老师

通过给定一个班级名称，可以查到一条班级记录，根据班级ID，又可以查到多条学生记录，这样，二维表之间就通过ID映射建立了“一对多”关系。

数据类型

对于一个关系表，除了定义每一列的名称外，还需要定义每一列的数据类型。关系数据库支持的标准数据类型包括数值、字符串、时间等：

名称	类型	说明
INT	整型	4字节整数类型，范围约+/-21亿
BIGINT	长整型	8字节整数类型，范围约+/-922亿亿
REAL	浮点型	4字节浮点数，范围约+/-1038
DOUBLE	浮点型	8字节浮点数，范围约+/-10308
DECIMAL(M,N)	高精度小数	由用户指定精度的小数，例如，DECIMAL(20,10)表示一共20位，其中小数10位，通常用于财务计算
CHAR(N)	定长字符串	存储指定长度的字符串，例如，CHAR(100)总是存储100个字符的字符串
VARCHAR(N)	变长字符串	存储可变长度的字符串，例如，VARCHAR(100)可以存储0~100个字符的字符串
BOOLEAN	布尔类型	存储True或者False
DATE	日期类型	存储日期，例如，2018-06-22
TIME	时间类型	存储时间，例如，12:20:59
DATETIME	日期和时间类型	存储日期+时间，例如，2018-06-22 12:20:59

上面的表中列举了最常用的数据类型。很多数据类型还有别名，例如，REAL又可以写成FLOAT(24)。还有一些不常用的数据类型，例如，TINYINT（范围在0~255）。各数据库厂商还会支持特定的数据类型，例如JSON。

选择数据类型的时候，要根据业务规则选择合适的类型。通常来说，BIGINT能满足整数存储的需求，VARCHAR(N)能满足字符串存储的需求，这两种类型是使用最广泛的。

主流关系数据库

目前，主流的关系数据库主要分为以下几类：

商用数据库，例如：Oracle，SQL Server，DB2等；
开源数据库，例如：MySQL，PostgreSQL等；
桌面数据库，以微软Access为代表，适合桌面应用程序使用；
嵌入式数据库，以Sqlite为代表，适合手机应用和桌面程序。

SQL

什么是SQL？SQL是结构化查询语言的缩写，用来访问和操作数据库系统。SQL语句既可以查询数据库中的数据，也可以添加、更新和删除数据库中的数据，还可以对数据库进行管理和维护操作。不同的数据库，都支持SQL，这样，我们通过学习SQL这一种语言，就可以操作各种不同的数据库。

虽然SQL已经被ANSI组织定义为标准，不幸地是，各个不同的数据库对标准的SQL支持不太一致。并且，大部分数据库都在标准的SQL上做了扩展。也就是说，如果只使用标准SQL，理论上所有数据库都可以支持，但如果使用某个特定数据库的扩展SQL，换一个数据库就不能执行了。例如，Oracle把自己扩展的SQL称为PL/SQL，Microsoft把自己扩展的SQL称为T-SQL。

现实情况是，如果我们只使用标准SQL的核心功能，那么所有数据库通常都可以执行。不常用的SQL功能，不同的数据库支持的程度都不一样。而各个数据库支持的各自扩展的功能，通常我们把它们称之为“方言”。

总的来说，SQL语言定义了这么几种操作数据库的能力：

DDL：Data Definition Language

DDL允许用户定义数据，也就是创建表、删除表、修改表结构这些操作。通常，DDL由数据库管理员执行。

DML：Data Manipulation Language

DML为用户提供添加、删除、更新数据的能力，这些是应用程序对数据库的日常操作。

DQL：Data Query Language

DQL允许用户查询数据，这也是通常最频繁的数据库日常操作。

语法特点

SQL语言关键字不区分大小写！！！但是，针对不同的数据库，对于表名和列名，有的数据库区分大小写，有的数据库不区分大小写。同一个数据库，有的在Linux上区分大小写，有的在Windows上不区分大小写。

所以，本教程约定：SQL关键字总是大写，以示突出，表名和列名均使用小写。

MySQL是目前应用最广泛的开源关系数据库。MySQL最早是由瑞典的MySQL AB公司开发，该公司在2008年被SUN公司收购，紧接着，SUN公司在2009年被Oracle公司收购，所以MySQL最终就变成了Oracle旗下的产品。

和其他关系数据库有所不同的是，MySQL本身实际上只是一个SQL接口，它的内部还包含了多种数据引擎，常用的包括：

InnoDB：由Innobase Oy公司开发的一款支持事务的数据库引擎，2006年被Oracle收购；
MyISAM：MySQL早期集成的默认数据库引擎，不支持事务。

MySQL接口和数据库引擎的关系就好比某某浏览器和浏览器引擎（IE引擎或Webkit引擎）的关系。对用户而言，切换浏览器引擎不影响浏览器界面，切换MySQL引擎不影响自己写的应用程序使用MySQL的接口。

使用MySQL时，不同的表还可以使用不同的数据库引擎。如果你不知道应该采用哪种引擎，记住总是选择InnoDB就好了。

因为MySQL一开始就是开源的，所以基于MySQL的开源版本，又衍生出了各种版本：

MariaDB

由MySQL的创始人创建的一个开源分支版本，使用XtraDB引擎。

Aurora

由Amazon改进的一个MySQL版本，专门提供给在AWS托管MySQL用户，号称5倍的性能提升。

PolarDB

由Alibaba改进的一个MySQL版本，专门提供给在阿里云托管的MySQL用户，号称6倍的性能提升。

而MySQL官方版本又分了好几个版本：

Community Edition：社区开源版本，免费；
Standard Edition：标准版；
Enterprise Edition：企业版；
Cluster Carrier Grade Edition：集群版。

以上版本的功能依次递增，价格也依次递增。不过，功能增加的主要是监控、集群等管理功能，对于基本的SQL功能是完全一样的。

所以使用MySQL就带来了一个巨大的好处：可以在自己的电脑上安装免费的Community Edition版本，进行学习、开发、测试，部署的时候，可以选择付费的高级版本，或者云服务商提供的兼容版本，而不需要对应用程序本身做改动。

安装MySQL

要安装MySQL，可以从MySQL官方网站下载最新的MySQL Community Server版本：

https://dev.mysql.com/downloads/mysql/

选择对应的操作系统版本，下载安装即可。在安装过程中，MySQL会自动创建一个root用户，并提示输入root口令。

要在Linux上安装MySQL，可以使用发行版的包管理器。例如，Debian和Ubuntu用户可以简单地通过命令apt install mysql-server安装最新的MySQL版本。

MySQL安装后会自动在后台运行。为了验证MySQL安装是否正确，我们需要通过mysql这个命令行程序来连接MySQL服务器。

在命令提示符下输入mysql -u root -p，然后输入口令，如果一切正确，就会连接到MySQL服务器，同时提示符变为mysql>。

输入exit退出MySQL命令行。注意，MySQL服务器仍在后台运行。

使用Docker运行MySQL

另一种运行MySQL的方式不需要下载安装包，而是直接通过Docker安装最新的MySQL：

首先安装Docker Desktop，然后在命令行输入以下命令拉取MySQL最新版：

1	$ docker pull mysql

拉取完成后，输入以下命令直接启动MySQL服务器：

1	$ docker run -d --name mysql -p 3306:3306 -e MYSQL_ROOT_PASSWORD=password -v /Users/chankein/mysql-data:/var/lib/mysql mysql

命令docker run表示启动一个容器，后面各参数含义如下：

-d：表示在后台执行；
--name mysql：表示容器的名字，不输入Docker会自动选择一个名字；
-p 3306:3306：表示把容器的端口3306映射到本机，这样可以在本机通过3306端口连接MySQL；
-e MYSQL_ROOT_PASSWORD=password：表示传入一个环境变量，作为root的口令，这里设置的口令是password，不输入此项则会自动生成一个口令，需要查看日志才能知道口令；
-v /Users/chankein/mysql-data:/var/lib/mysql：表示将本地目录映射到容器目录/var/lib/mysql作为MySQL数据库存放的位置，需要将/Users/chankein/mysql-data改为你的电脑上的实际目录；
mysql：最后一个参数是Docker镜像的名称。

可以在Docker Desktop的管理窗口中选择Containers，看到正在运行的MySQL：

docker-mysql

点击MySQL查看日志：

docker-mysql-log

点击Exec进入命令行，输入命令mysql -u root -p，输入口令，即可进入MySQL命令行界面：

docker-mysql-exec

使用Docker运行MySQL时，任何时候都可以删除MySQL容器并重新运行。如果删除了本地映射的目录，重新运行就相当于一个全新的MySQL，因此，建议仅作为学习和开发使用，不要存储重要的数据。

关系模型

我们已经知道，关系数据库是建立在关系模型上的。而关系模型本质上就是若干个存储数据的二维表，可以把它们看作很多Excel表。

表的每一行称为记录（Record），记录是一个逻辑意义上的数据。

表的每一列称为字段（Column），同一个表的每一行记录都拥有相同的若干字段。

字段定义了数据类型（整型、浮点型、字符串、日期等），以及是否允许为NULL。注意NULL表示字段数据不存在。一个整型字段如果为NULL不表示它的值为0，同样的，一个字符串型字段为NULL也不表示它的值为空串''。

提示

通常情况下，字段应该避免允许为NULL。不允许为NULL可以简化查询条件，加快查询速度，也利于应用程序读取数据后无需判断是否为NULL。

和Excel表有所不同的是，关系数据库的表和表之间需要建立“一对多”，“多对一”和“一对一”的关系，这样才能够按照应用程序的逻辑来组织和存储数据。

例如，一个班级表：

ID	名称	班主任
201	二年级一班	王老师
202	二年级二班	李老师

每一行对应着一个班级，而一个班级对应着多个学生，所以班级表和学生表的关系就是“一对多”：

ID	姓名	班级ID	性别	年龄
1	小明	201	M	9
2	小红	202	F	8
3	小军	202	M	8
4	小白	201	F	9

反过来，如果我们先在学生表中定位了一行记录，例如ID=1的小明，要确定他的班级，只需要根据他的“班级ID”对应的值201找到班级表中ID=201的记录，即二年级一班。所以，学生表和班级表是“多对一”的关系。

如果我们把班级表分拆得细一点，例如，单独创建一个教师表：

ID	名称	年龄
A1	王老师	26
A2	张老师	39
A3	李老师	32
A4	赵老师	27

班级表只存储教师ID：

ID	名称	班主任ID
201	二年级一班	A1
202	二年级二班	A3

这样，一个班级总是对应一个教师，班级表和教师表就是“一对一”关系。

在关系数据库中，关系是通过主键和外键来维护的。我们在后面会分别深入讲解。

主键

在关系数据库中，一张表中的每一行数据被称为一条记录。一条记录就是由多个字段组成的。例如，students表的两行记录：

id	class_id	name	gender	score
1	1	小明	M	90
2	1	小红	F	95

每一条记录都包含若干定义好的字段。同一个表的所有记录都有相同的字段定义。

对于关系表，有个很重要的约束，就是任意两条记录不能重复。不能重复不是指两条记录不完全相同，而是指能够通过某个字段唯一区分出不同的记录，这个字段被称为主键。

例如，假设我们把name字段作为主键，那么通过名字小明或小红就能唯一确定一条记录。但是，这么设定，就没法存储同名的同学了，因为插入相同主键的两条记录是不被允许的。

对主键的要求，最关键的一点是：记录一旦插入到表中，主键最好不要再修改，因为主键是用来唯一定位记录的，修改了主键，会造成一系列的影响。

由于主键的作用十分重要，如何选取主键会对业务开发产生重要影响。如果我们以学生的身份证号作为主键，似乎能唯一定位记录。然而，身份证号也是一种业务场景，如果身份证号升位了，或者需要变更，作为主键，不得不修改的时候，就会对业务产生严重影响。

所以，选取主键的一个基本原则是：不使用任何业务相关的字段作为主键。

因此，身份证号、手机号、邮箱地址这些看上去可以唯一的字段，均不可用作主键。

作为主键最好是完全业务无关的字段，我们一般把这个字段命名为id。常见的可作为id字段的类型有：

自增整数类型：数据库会在插入数据时自动为每一条记录分配一个自增整数，这样我们就完全不用担心主键重复，也不用自己预先生成主键；
全局唯一GUID类型：也称UUID，使用一种全局唯一的字符串作为主键，类似8f55d96b-8acc-4636-8cb8-76bf8abc2f57。GUID算法通过网卡MAC地址、时间戳和随机数保证任意计算机在任意时间生成的字符串都是不同的，大部分编程语言都内置了GUID算法，可以自己预算出主键。

对于大部分应用来说，通常自增类型的主键就能满足需求。我们在students表中定义的主键也是BIGINT NOT NULL AUTO_INCREMENT类型。

注意

如果使用INT自增类型，那么当一张表的记录数超过2147483647（约21亿）时，会达到上限而出错。使用BIGINT自增类型则可以最多约922亿亿条记录。

联合主键

关系数据库实际上还允许通过多个字段唯一标识记录，即两个或更多的字段都设置为主键，这种主键被称为联合主键。

对于联合主键，允许一列有重复，只要不是所有主键列都重复即可：

id_num	id_type	other columns…
1	A	…
2	A	…
2	B	…

如果我们把上述表的id_num和id_type这两列作为联合主键，那么上面的3条记录都是允许的，因为没有两列主键组合起来是相同的。

没有必要的情况下，我们尽量不使用联合主键，因为它给关系表带来了复杂度的上升。

小结

主键是关系表中记录的唯一标识。主键的选取非常重要：主键不要带有业务含义，而应该使用BIGINT自增或者GUID类型。主键也不应该允许NULL。

可以使用多个列作为联合主键，但联合主键并不常用。

当我们用主键唯一标识记录时，我们就可以在students表中确定任意一个学生的记录：

id	name	other columns…
1	小明	…
2	小红	…

我们还可以在classes表中确定任意一个班级记录：

id	name	other columns…
1	一班	…
2	二班	…

但是我们如何确定students表的一条记录，例如，id=1的小明，属于哪个班级呢？

由于一个班级可以有多个学生，在关系模型中，这两个表的关系可以称为“一对多”，即一个classes的记录可以对应多个students表的记录。

为了表达这种一对多的关系，我们需要在students表中加入一列class_id，让它的值与classes表的某条记录相对应：

id	class_id	name	other columns…
1	1	小明	…
2	1	小红	…
5	2	小白	…

这样，我们就可以根据class_id这个列直接定位出一个students表的记录应该对应到classes的哪条记录。

例如：

小明的class_id是1，因此，对应的classes表的记录是id=1的一班；
小红的class_id是1，因此，对应的classes表的记录是id=1的一班；
小白的class_id是2，因此，对应的classes表的记录是id=2的二班。

在students表中，通过class_id的字段，可以把数据与另一张表关联起来，这种列称为外键。

外键并不是通过列名实现的，而是通过定义外键约束实现的：

ALTER TABLE students
ADD CONSTRAINT fk_class_id
FOREIGN KEY (class_id)
REFERENCES classes (id);

其中，外键约束的名称fk_class_id可以任意，FOREIGN KEY (class_id)指定了class_id作为外键，REFERENCES classes (id)指定了这个外键将关联到classes表的id列（即classes表的主键）。

通过定义外键约束，关系数据库可以保证无法插入无效的数据。即如果classes表不存在id=99的记录，students表就无法插入class_id=99的记录。

由于外键约束会降低数据库的性能，大部分互联网应用程序为了追求速度，并不设置外键约束，而是仅靠应用程序自身来保证逻辑的正确性。这种情况下，class_id仅仅是一个普通的列，只是它起到了外键的作用而已。

要删除一个外键约束，也是通过ALTER TABLE实现的：

1 2	ALTER TABLE students DROP FOREIGN KEY fk_class_id;

注意：删除外键约束并没有删除外键这一列。删除列是通过DROP COLUMN ...实现的。

多对多

通过一个表的外键关联到另一个表，我们可以定义出一对多关系。有些时候，还需要定义“多对多”关系。例如，一个老师可以对应多个班级，一个班级也可以对应多个老师，因此，班级表和老师表存在多对多关系。

多对多关系实际上是通过两个一对多关系实现的，即通过一个中间表，关联两个一对多关系，就形成了多对多关系：

teachers表：

id	name
1	张老师
2	王老师
3	李老师
4	赵老师

classes表：

id	name
1	一班
2	二班

中间表teacher_class关联两个一对多关系：

id	teacher_id	class_id
1	1	1
2	1	2
3	2	1
4	2	2
5	3	1
6	4	2

通过中间表teacher_class可知teachers到classes的关系：

id=1的张老师对应id=1,2的一班和二班；
id=2的王老师对应id=1,2的一班和二班；
id=3的李老师对应id=1的一班；
id=4的赵老师对应id=2的二班。

同理可知classes到teachers的关系：

id=1的一班对应id=1,2,3的张老师、王老师和李老师；
id=2的二班对应id=1,2,4的张老师、王老师和赵老师；

因此，通过中间表，我们就定义了一个“多对多”关系。

一对一

一对一关系是指，一个表的记录对应到另一个表的唯一一个记录。

例如，students表的每个学生可以有自己的联系方式，如果把联系方式存入另一个表contacts，我们就可以得到一个“一对一”关系：

id	student_id	mobile
1	1	135xxxx6300
2	2	138xxxx2209
3	5	139xxxx8086

有细心的童鞋会问，既然是一对一关系，那为啥不给students表增加一个mobile列，这样就能合二为一了？

如果业务允许，完全可以把两个表合为一个表。但是，有些时候，如果某个学生没有手机号，那么，contacts表就不存在对应的记录。实际上，一对一关系准确地说，是contacts表一对一对应students表。

还有一些应用会把一个大表拆成两个一对一的表，目的是把经常读取和不经常读取的字段分开，以获得更高的性能。例如，把一个大的用户表分拆为用户基本信息表user_info和用户详细信息表user_profiles，大部分时候，只需要查询user_info表，并不需要查询user_profiles表，这样就提高了查询速度。

小结

关系数据库通过外键可以实现一对多、多对多和一对一的关系。外键既可以通过数据库来约束，也可以不设置约束，仅依靠应用程序的逻辑来保证。

在关系数据库中，如果有上万甚至上亿条记录，在查找记录的时候，想要获得非常快的速度，就需要使用索引。

索引是关系数据库中对某一列或多个列的值进行预排序的数据结构。通过使用索引，可以让数据库系统不必扫描整个表，而是直接定位到符合条件的记录，这样就大大加快了查询速度。

例如，对于students表：

id	class_id	name	gender	score
1	1	小明	M	90
2	1	小红	F	95
3	1	小军	M	88

如果要经常根据score列进行查询，就可以对score列创建索引：

1 2	ALTER TABLE students ADD INDEX idx_score (score);

使用ADD INDEX idx_score (score)就创建了一个名称为idx_score，使用列score的索引。索引名称是任意的，索引如果有多列，可以在括号里依次写上，例如：

1 2	ALTER TABLE students ADD INDEX idx_name_score (name, score);

索引的效率取决于索引列的值是否散列，即该列的值如果越互不相同，那么索引效率越高。反过来，如果记录的列存在大量相同的值，例如gender列，大约一半的记录值是M，另一半是F，因此，对该列创建索引就没有意义。

可以对一张表创建多个索引。索引的优点是提高了查询效率，缺点是在插入、更新和删除记录时，需要同时修改索引，因此，索引越多，插入、更新和删除记录的速度就越慢。

对于主键，关系数据库会自动对其创建主键索引。使用主键索引的效率是最高的，因为主键会保证绝对唯一。

唯一索引

在设计关系数据表的时候，看上去唯一的列，例如身份证号、邮箱地址等，因为他们具有业务含义，因此不宜作为主键。

但是，这些列根据业务要求，又具有唯一性约束：即不能出现两条记录存储了同一个身份证号。这个时候，就可以给该列添加一个唯一索引。例如，我们假设students表的name不能重复：

1 2	ALTER TABLE students ADD UNIQUE INDEX uni_name (name);

通过UNIQUE关键字我们就添加了一个唯一索引。

也可以只对某一列添加一个唯一约束而不创建唯一索引：

1 2	ALTER TABLE students ADD CONSTRAINT uni_name UNIQUE (name);

这种情况下，name列没有索引，但仍然具有唯一性保证。

无论是否创建索引，对于用户和应用程序来说，使用关系数据库不会有任何区别。这里的意思是说，当我们在数据库中查询时，如果有相应的索引可用，数据库系统就会自动使用索引来提高查询效率，如果没有索引，查询也能正常执行，只是速度会变慢。因此，索引可以在使用数据库的过程中逐步优化。

小结

通过对数据库表创建索引，可以提高查询速度；

通过创建唯一索引，可以保证某一列的值具有唯一性；

数据库索引对于用户和应用程序来说都是透明的。

在关系数据库中，最常用的操作就是查询。

准备数据

为了便于讲解和练习，我们先准备好了一个students表和一个classes表，它们的结构和数据如下：

students表存储了学生信息：

id	class_id	name	gender	score
1	1	小明	M	90
2	1	小红	F	95
3	1	小军	M	88
4	1	小米	F	73
5	2	小白	F	81
6	2	小兵	M	55
7	2	小林	M	85
8	3	小新	F	91
9	3	小王	M	89
10	3	小丽	F	85

classes表存储了班级信息：

id	name
1	一班
2	二班
3	三班
4	四班

请注意，和MySQL的持久化存储不同的是，由于我们使用的是AlaSQL内存数据库，两张表的数据在页面加载时导入，并且只存在于浏览器的内存中，因此，刷新页面后，数据会重置为上述初始值。

MySQL

如果你想用MySQL练习，可以下载这个SQL脚本，然后在命令行运行：

1	$ mysql -u root -p < init-test-data.sql

就可以自动创建test数据库，并且在test数据库下创建students表和classes表，以及必要的初始化数据。

和内存数据库不同的是，对MySQL数据库做的所有修改，都会保存下来。如果你希望恢复到初始状态，可以再次运行该脚本。

基本查询

要查询数据库表的数据，我们使用如下的SQL语句：

1	SELECT * FROM <表名>

假设表名是students，要查询students表的所有行，我们用如下SQL语句：

1 2	-- 查询students表的所有数据 SELECT * FROM students;

使用SELECT * FROM students时，SELECT是关键字，表示将要执行一个查询，*表示“所有列”，FROM表示将要从哪个表查询，本例中是students表。

该SQL将查询出students表的所有数据。注意：查询结果也是一个二维表，它包含列名和每一行的数据。

要查询classes表的所有行，我们用如下SQL语句：

1 2	-- 查询classes表的所有数据 SELECT * FROM classes;

运行上述SQL语句，观察查询结果。

SELECT语句其实并不要求一定要有FROM子句。我们来试试下面的SELECT语句：

1 2	-- 计算100+200 SELECT 100+200;

上述查询会直接计算出表达式的结果。虽然SELECT可以用作计算，但它并不是SQL的强项。但是，不带FROM子句的SELECT语句有一个有用的用途，就是用来判断当前到数据库的连接是否有效。许多检测工具会执行一条SELECT 1;来测试数据库连接。

小结

使用SELECT查询的基本语句SELECT * FROM <表名>可以查询一个表的所有行和所有列的数据；

SELECT查询的结果是一个二维表。

使用SELECT * FROM <表名>可以查询到一张表的所有记录。但是，很多时候，我们并不希望获得所有记录，而是根据条件选择性地获取指定条件的记录，例如，查询分数在80分以上的学生记录。在一张表有数百万记录的情况下，获取所有记录不仅费时，还费内存和网络带宽。

SELECT语句可以通过WHERE条件来设定查询条件，查询结果是满足查询条件的记录。例如，要指定条件“分数在80分或以上的学生”，写成WHERE条件就是SELECT * FROM students WHERE score >= 80。

其中，WHERE关键字后面的score >= 80就是条件。score是列名，该列存储了学生的成绩，因此，score >= 80就筛选出了指定条件的记录：

1 2	-- 按条件查询students: SELECT * FROM students WHERE score >= 80;

因此，条件查询的语法就是：

1	SELECT * FROM <表名> WHERE <条件表达式>

条件表达式可以用<条件1> AND <条件2>表达满足条件1并且满足条件2。例如，符合条件“分数在80分或以上”，并且还符合条件“男生”，把这两个条件写出来：

条件1：根据score列的数据判断：score >= 80；
条件2：根据gender列的数据判断：gender = 'M'，注意gender列存储的是字符串，需要用单引号括起来。

就可以写出WHERE条件：score >= 80 AND gender = 'M'：

1 2	-- 按AND条件查询students: SELECT * FROM students WHERE score >= 80 AND gender = 'M';

第二种条件是<条件1> OR <条件2>，表示满足条件1或者满足条件2。例如，把上述AND查询的两个条件改为OR，查询结果就是“分数在80分或以上”或者“男生”，满足任意之一的条件即选出该记录：

1 2	-- 按OR条件查询students: SELECT * FROM students WHERE score >= 80 OR gender = 'M';

很显然OR条件要比AND条件宽松，返回的符合条件的记录也更多。

第三种条件是NOT <条件>，表示“不符合该条件”的记录。例如，写一个“不是2班的学生”这个条件，可以先写出“是2班的学生”：class_id = 2，再加上NOT：NOT class_id = 2：

1 2	-- 按NOT条件查询students: SELECT * FROM students WHERE NOT class_id = 2;

上述NOT条件NOT class_id = 2其实等价于class_id <> 2，因此，NOT查询不是很常用。

要组合三个或者更多的条件，就需要用小括号()表示如何进行条件运算。例如，编写一个复杂的条件：分数在80以下或者90以上，并且是男生：

1 2	-- 按多个条件查询students: SELECT * FROM students WHERE (score < 80 OR score > 90) AND gender = 'M';

如果不加括号，条件运算按照NOT、AND、OR的优先级进行，即NOT优先级最高，其次是AND，最后是OR。加上括号可以改变优先级。

常用的条件表达式

条件	表达式举例1	表达式举例2	说明
使用=判断相等	score = 80	name = ‘abc’	字符串需要用单引号括起来
使用>判断大于	score > 80	name > ‘abc’	字符串比较根据ASCII码，中文字符比较根据数据库设置
使用>=判断大于或相等	score >= 80	name >= ‘abc’
使用<判断小于	score < 80	name <= ‘abc’
使用<=判断小于或相等	score <= 80	name <= ‘abc’
使用<>判断不相等	score <> 80	name <> ‘abc’
使用LIKE判断相似	name LIKE ‘ab%’	name LIKE ‘%bc%’	%表示任意字符，例如’ab%‘将匹配’ab’，‘abc’，‘abcd’

查询分数在60分(含)～90分(含)之间的学生可以使用的WHERE语句是：

小结

通过WHERE条件查询，可以筛选出符合指定条件的记录，而不是整个表的所有记录。

投影查询

使用SELECT * FROM <表名> WHERE <条件>可以选出表中的若干条记录。我们注意到返回的二维表结构和原表是相同的，即结果集的所有列与原表的所有列都一一对应。

如果我们只希望返回某些列的数据，而不是所有列的数据，我们可以用SELECT 列1, 列2, 列3 FROM ...，让结果集仅包含指定列。这种操作称为投影查询。

例如，从students表中返回id、score和name这三列：

1 2	-- 使用投影查询 SELECT id, score, name FROM students;

这样返回的结果集就只包含了我们指定的列，并且，结果集的列的顺序和原表可以不一样。

使用SELECT 列1, 列2, 列3 FROM ...时，还可以给每一列起个别名，这样，结果集的列名就可以与原表的列名不同。它的语法是SELECT 列1 别名1, 列2 别名2, 列3 别名3 FROM ...。

例如，以下SELECT语句将列名score重命名为points，而id和name列名保持不变：

1 2	-- 使用投影查询，并将列名重命名： SELECT id, score points, name FROM students;

投影查询同样可以接WHERE条件，实现复杂的查询：

1 2	-- 使用投影查询+WHERE条件： SELECT id, score points, name FROM students WHERE gender = 'M';

小结

使用SELECT *表示查询表的所有列，使用SELECT 列1, 列2, 列3则可以仅返回指定列，这种操作称为投影；

SELECT语句可以对结果集的列进行重命名。

排序

我们使用SELECT查询时，细心的读者可能注意到，查询结果集通常是按照id排序的，也就是根据主键排序。这也是大部分数据库的做法。如果我们要根据其他条件排序怎么办？可以加上ORDER BY子句。例如按照成绩从低到高进行排序：

1 2	-- 按score从低到高: SELECT id, name, gender, score FROM students ORDER BY score;

如果要反过来，按照成绩从高到底排序，我们可以加上DESC表示“倒序”：

1 2	-- 按score从高到低: SELECT id, name, gender, score FROM students ORDER BY score DESC;

如果score列有相同的数据，要进一步排序，可以继续添加列名。例如，使用ORDER BY score DESC, gender表示先按score列倒序，如果有相同分数的，再按gender列排序：

1 2	-- 按score, gender排序: SELECT id, name, gender, score FROM students ORDER BY score DESC, gender;

默认的排序规则是ASC：“升序”，即从小到大。ASC可以省略，即ORDER BY score ASC和ORDER BY score效果一样。

如果有WHERE子句，那么ORDER BY子句要放到WHERE子句后面。例如，查询一班的学生成绩，并按照倒序排序：

-- 带WHERE条件的ORDER BY:
SELECT id, name, gender, score
FROM students
WHERE class_id = 1
ORDER BY score DESC;

这样，结果集仅包含符合WHERE条件的记录，并按照ORDER BY的设定排序。

小结

使用ORDER BY可以对结果集进行排序；

可以对多列进行升序、倒序排序。

使用SELECT查询时，如果结果集数据量很大，比如几万行数据，放在一个页面显示的话数据量太大，不如分页显示，每次显示100条。

要实现分页功能，实际上就是从结果集中显示第1~100条记录作为第1页，显示第101~200条记录作为第2页，以此类推。

因此，分页实际上就是从结果集中“截取”出第M~N条记录。这个查询可以通过LIMIT <N-M> OFFSET <M>子句实现。我们先把所有学生按照成绩从高到低进行排序：

1 2	-- 按score从高到低: SELECT id, name, gender, score FROM students ORDER BY score DESC;

现在，我们把结果集分页，每页3条记录。要获取第1页的记录，可以使用LIMIT 3 OFFSET 0：

-- 查询第1页:
SELECT id, name, gender, score
FROM students
ORDER BY score DESC
LIMIT 3 OFFSET 0;

上述查询LIMIT 3 OFFSET 0表示，对结果集从0号记录开始，最多取3条。注意SQL记录集的索引从0开始。

如果要查询第2页，那么我们只需要“跳过”头3条记录，也就是对结果集从3号记录开始查询，把OFFSET设定为3：

-- 查询第2页:
SELECT id, name, gender, score
FROM students
ORDER BY score DESC
LIMIT 3 OFFSET 3;

类似的，查询第3页的时候，OFFSET应该设定为6:

-- 查询第3页:
SELECT id, name, gender, score
FROM students
ORDER BY score DESC
LIMIT 3 OFFSET 6;

查询第4页的时候，OFFSET应该设定为9:

-- 查询第4页:
SELECT id, name, gender, score
FROM students
ORDER BY score DESC
LIMIT 3 OFFSET 9;

由于第4页只有1条记录，因此最终结果集按实际数量1显示。LIMIT 3表示的意思是“最多3条记录”。

可见，分页查询的关键在于，首先要确定每页需要显示的结果数量pageSize（这里是3），然后根据当前页的索引pageIndex（从1开始），确定LIMIT和OFFSET应该设定的值：

LIMIT总是设定为pageSize；
OFFSET计算公式为pageSize * (pageIndex - 1)。

这样就能正确查询出第N页的记录集。

如果原本记录集一共就10条记录，但我们把OFFSET设置为20，会得到什么结果呢？

-- OFFSET设定为20:
SELECT id, name, gender, score
FROM students
ORDER BY score DESC
LIMIT 3 OFFSET 20;

OFFSET超过了查询的最大数量并不会报错，而是得到一个空的结果集。

注意

OFFSET是可选的，如果只写LIMIT 15，那么相当于LIMIT 15 OFFSET 0。

在MySQL中，LIMIT 15 OFFSET 30还可以简写成LIMIT 30, 15。

使用LIMIT <M> OFFSET <N>分页时，随着N越来越大，查询效率也会越来越低。

思考

在分页查询之前，如何计算一共有几页？

小结

使用LIMIT <M> OFFSET <N>可以对结果集进行分页，每次查询返回结果集的一部分；

分页查询需要先确定每页的数量和当前页数，然后确定LIMIT和OFFSET的值。

如果我们要统计一张表的数据量，例如，想查询students表一共有多少条记录，难道必须用SELECT * FROM students查出来然后再数一数有多少行吗？

这个方法当然可以，但是比较弱智。对于统计总数、平均数这类计算，SQL提供了专门的聚合函数，使用聚合函数进行查询，就是聚合查询，它可以快速获得结果。

仍然以查询students表一共有多少条记录为例，我们可以使用SQL内置的COUNT()函数查询：

1 2	-- 使用聚合查询: SELECT COUNT(*) FROM students;

COUNT(*)表示查询所有列的行数，要注意聚合的计算结果虽然是一个数字，但查询的结果仍然是一个二维表，只是这个二维表只有一行一列，并且列名是COUNT(*)。

通常，使用聚合查询时，我们应该给列名设置一个别名，便于处理结果：

1 2	-- 使用聚合查询并设置结果集的列名为num: SELECT COUNT(*) num FROM students;

COUNT(*)和COUNT(id)实际上是一样的效果。另外注意，聚合查询同样可以使用WHERE条件，因此我们可以方便地统计出有多少男生、多少女生、多少80分以上的学生等：

1 2	-- 使用聚合查询并设置WHERE条件: SELECT COUNT(*) boys FROM students WHERE gender = 'M';

除了COUNT()函数外，SQL还提供了如下聚合函数：

函数	说明
SUM	计算某一列的合计值，该列必须为数值类型
AVG	计算某一列的平均值，该列必须为数值类型
MAX	计算某一列的最大值
MIN	计算某一列的最小值

注意，MAX()和MIN()函数并不限于数值类型。如果是字符类型，MAX()和MIN()会返回排序最后和排序最前的字符。

要统计男生的平均成绩，我们用下面的聚合查询：

1 2	-- 使用聚合查询计算男生平均成绩: SELECT AVG(score) average FROM students WHERE gender = 'M';

要特别注意：如果聚合查询的WHERE条件没有匹配到任何行，COUNT()会返回0，而SUM()、AVG()、MAX()和MIN()会返回NULL：

1 2	-- WHERE条件gender = 'X'匹配不到任何行: SELECT AVG(score) average FROM students WHERE gender = 'X';

分组

如果我们要统计一班的学生数量，我们知道，可以用SELECT COUNT(*) num FROM students WHERE class_id = 1;。如果要继续统计二班、三班的学生数量，难道必须不断修改WHERE条件来执行SELECT语句吗？

对于聚合查询，SQL还提供了“分组聚合”的功能。我们观察下面的聚合查询：

1 2	-- 按class_id分组: SELECT COUNT(*) num FROM students GROUP BY class_id;

执行这个查询，COUNT()的结果不再是一个，而是3个，这是因为，GROUP BY子句指定了按class_id分组，因此，执行该SELECT语句时，会把class_id相同的列先分组，再分别计算，因此，得到了3行结果。

但是这3行结果分别是哪三个班级的，不好看出来，所以我们可以把class_id列也放入结果集中：

1 2	-- 按class_id分组: SELECT class_id, COUNT(*) num FROM students GROUP BY class_id;

这下结果集就可以一目了然地看出各个班级的学生人数。我们再试试把name放入结果集：

1 2	-- 按class_id分组: SELECT name, class_id, COUNT(*) num FROM students GROUP BY class_id;

不出意外，执行这条查询我们会得到一个语法错误，因为在任意一个分组中，只有class_id都相同，name是不同的，SQL引擎不能把多个name的值放入一行记录中。因此，聚合查询的列中，只能放入分组的列。

注意

AlaSQL并没有严格执行SQL标准，上述SQL在浏览器可以正常执行，但是在MySQL、Oracle等环境下将报错，请自行在MySQL中测试。

也可以使用多个列进行分组。例如，我们想统计各班的男生和女生人数：

1 2	-- 按class_id, gender分组: SELECT class_id, gender, COUNT(*) num FROM students GROUP BY class_id, gender;

上述查询结果集一共有6条记录，分别对应各班级的男生和女生人数。

练习

请使用一条SELECT查询查出每个班级的平均分：

1 2	-- 查出每个班级的平均分，结果集应当有3条记录: SELECT 'TODO';

请使用一条SELECT查询查出每个班级男生和女生的平均分：

1 2	-- 查出每个班级的平均分，结果集应当有6条记录: SELECT 'TODO';

小结

使用SQL提供的聚合查询，我们可以方便地计算总数、合计值、平均值、最大值和最小值；

聚合查询可以用GROUP BY分组聚合；

聚合查询也可以添加WHERE条件。

SELECT查询不但可以从一张表查询数据，还可以从多张表同时查询数据。查询多张表的语法是：SELECT * FROM <表1> <表2>。

例如，同时从students表和classes表的“乘积”，即查询数据，可以这么写：

1 2	-- FROM students, classes: SELECT * FROM students, classes;

这种一次查询两个表的数据，查询的结果也是一个二维表，它是students表和classes表的“乘积”，即students表的每一行与classes表的每一行都两两拼在一起返回。结果集的列数是students表和classes表的列数之和，行数是students表和classes表的行数之积。

这种多表查询又称笛卡尔查询，使用笛卡尔查询时要非常小心，由于结果集是目标表的行数乘积，对两个各自有100行记录的表进行笛卡尔查询将返回1万条记录，对两个各自有1万行记录的表进行笛卡尔查询将返回1亿条记录。

你可能还注意到了，上述查询的结果集有两列id和两列name，两列id是因为其中一列是students表的id，而另一列是classes表的id，但是在结果集中，不好区分。两列name同理

要解决这个问题，我们仍然可以利用投影查询的“设置列的别名”来给两个表各自的id和name列起别名：

-- set alias:
SELECT
    students.id sid,
    students.name,
    students.gender,
    students.score,
    classes.id cid,
    classes.name cname
FROM students, classes;

注意，多表查询时，要使用表名.列名这样的方式来引用列和设置别名，这样就避免了结果集的列名重复问题。但是，用表名.列名这种方式列举两个表的所有列实在是很麻烦，所以SQL还允许给表设置一个别名，让我们在投影查询中引用起来稍微简洁一点：

-- set table alias:
SELECT
    s.id sid,
    s.name,
    s.gender,
    s.score,
    c.id cid,
    c.name cname
FROM students s, classes c;

注意到FROM子句给表设置别名的语法是FROM <表名1> <别名1>, <表名2> <别名2>。这样我们用别名s和c分别表示students表和classes表。

多表查询也是可以添加WHERE条件的，我们来试试：

-- set where clause:
SELECT
    s.id sid,
    s.name,
    s.gender,
    s.score,
    c.id cid,
    c.name cname
FROM students s, classes c
WHERE s.gender = 'M' AND c.id = 1;

这个查询的结果集每行记录都满足条件s.gender = 'M'和c.id = 1。添加WHERE条件后结果集的数量大大减少了。

小结

使用多表查询可以获取M x N行记录；

多表查询的结果集可能非常巨大，要小心使用。

连接查询是另一种类型的多表查询。连接查询对多个表进行JOIN运算，简单地说，就是先确定一个主表作为结果集，然后，把其他表的行有选择性地“连接”在主表结果集上。

例如，我们想要选出students表的所有学生信息，可以用一条简单的SELECT语句完成：

1 2	-- 选出所有学生: SELECT s.id, s.name, s.class_id, s.gender, s.score FROM students s;

但是，假设我们希望结果集同时包含所在班级的名称，上面的结果集只有class_id列，缺少对应班级的name列。

现在问题来了，存放班级名称的name列存储在classes表中，只有根据students表的class_id，找到classes表对应的行，再取出name列，就可以获得班级名称。

这时，连接查询就派上了用场。我们先使用最常用的一种内连接——INNER JOIN来实现：

-- 选出所有学生，同时返回班级名称:
SELECT s.id, s.name, s.class_id, c.name class_name, s.gender, s.score
FROM students s
INNER JOIN classes c
ON s.class_id = c.id;

注意INNER JOIN查询的写法是：

先确定主表，仍然使用FROM <表1>的语法；
再确定需要连接的表，使用INNER JOIN <表2>的语法；
然后确定连接条件，使用ON <条件...>，这里的条件是s.class_id = c.id，表示students表的class_id列与classes表的id列相同的行需要连接；
可选：加上WHERE子句、ORDER BY等子句。

使用别名不是必须的，但可以更好地简化查询语句。

那什么是内连接（INNER JOIN）呢？先别着急，有内连接（INNER JOIN）就有外连接（OUTER JOIN）。我们把内连接查询改成外连接查询，看看效果：

-- 使用OUTER JOIN:
SELECT s.id, s.name, s.class_id, c.name class_name, s.gender, s.score
FROM students s
RIGHT OUTER JOIN classes c
ON s.class_id = c.id;

执行上述RIGHT OUTER JOIN可以看到，和INNER JOIN相比，RIGHT OUTER JOIN多了一行，多出来的一行是“四班”，但是，学生相关的列如name、gender、score都为NULL。

这也容易理解，因为根据ON条件s.class_id = c.id，classes表的id=4的行正是“四班”，但是，students表中并不存在class_id=4的行。

有RIGHT OUTER JOIN，就有LEFT OUTER JOIN，以及FULL OUTER JOIN。它们的区别是：

INNER JOIN只返回同时存在于两张表的行数据，由于students表的class_id包含1，2，3，classes表的id包含1，2，3，4，所以，INNER JOIN根据条件s.class_id = c.id返回的结果集仅包含1，2，3。

RIGHT OUTER JOIN返回右表都存在的行。如果某一行仅在右表存在，那么结果集就会以NULL填充剩下的字段。

LEFT OUTER JOIN则返回左表都存在的行。如果我们给students表增加一行，并添加class_id=5，由于classes表并不存在id=5的行，所以，LEFT OUTER JOIN的结果会增加一行，对应的class_name是NULL：

-- 先增加一列class_id=5:
INSERT INTO students (class_id, name, gender, score) values (5, '新生', 'M', 88);
-- 使用LEFT OUTER JOIN:
SELECT s.id, s.name, s.class_id, c.name class_name, s.gender, s.score
FROM students s
LEFT OUTER JOIN classes c
ON s.class_id = c.id;

最后，我们使用FULL OUTER JOIN，它会把两张表的所有记录全部选择出来，并且，自动把对方不存在的列填充为NULL：

-- 使用FULL OUTER JOIN:
SELECT s.id, s.name, s.class_id, c.name class_name, s.gender, s.score
FROM students s
FULL OUTER JOIN classes c
ON s.class_id = c.id;

对于这么多种JOIN查询，到底什么使用应该用哪种呢？其实我们用图来表示结果集就一目了然了。

假设查询语句是：

1	SELECT ... FROM tableA ??? JOIN tableB ON tableA.column1 = tableB.column2;

我们把tableA看作左表，把tableB看成右表，那么INNER JOIN是选出两张表都存在的记录：

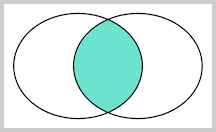
inner-join

LEFT OUTER JOIN是选出左表存在的记录：

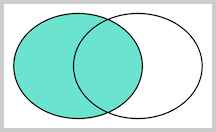
left-outer-join

RIGHT OUTER JOIN是选出右表存在的记录：

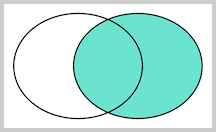
right-outer-join

FULL OUTER JOIN则是选出左右表都存在的记录：

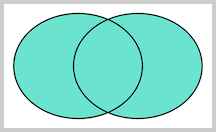
full-outer-join

小结

JOIN查询需要先确定主表，然后把另一个表的数据“附加”到结果集上；

INNER JOIN是最常用的一种JOIN查询，它的语法是SELECT ... FROM <表1> INNER JOIN <表2> ON <条件...>；

JOIN查询仍然可以使用WHERE条件和ORDER BY排序。

关系数据库的基本操作就是增删改查，即CRUD：Create、Retrieve、Update、Delete。其中，对于查询，我们已经详细讲述了SELECT语句的详细用法。

而对于增、删、改，对应的SQL语句分别是：

INSERT：插入新记录；
UPDATE：更新已有记录；
DELETE：删除已有记录。

我们将分别讨论这三种修改数据的语句的使用方法。

插入数据

当我们需要向数据库表中插入一条新记录时，就必须使用INSERT语句。

INSERT语句的基本语法是：

1	INSERT INTO <表名> (字段1, 字段2, ...) VALUES (值1, 值2, ...);

例如，我们向students表插入一条新记录，先列举出需要插入的字段名称，然后在VALUES子句中依次写出对应字段的值：

-- 添加一条新记录:
INSERT INTO students (class_id, name, gender, score) VALUES (2, '大牛', 'M', 80);
-- 查询并观察结果:
SELECT * FROM students;

注意到我们并没有列出id字段，也没有列出id字段对应的值，这是因为id字段是一个自增主键，它的值可以由数据库自己推算出来。此外，如果一个字段有默认值，那么在INSERT语句中也可以不出现。

要注意，INSERT字段顺序不必和数据库表的字段顺序一致，但值的顺序必须和INSERT字段顺序一致。也就是说，可以写INSERT INTO students (score, gender, name, class_id) ...，但是对应的VALUES就得变成(80, 'M', '大牛', 2)。

还可以一次性添加多条记录，只需要在VALUES子句中指定多个记录值，每个记录是由(...)包含的一组值，每组值用逗号,分隔：

-- 一次性添加多条新记录:
INSERT INTO students (class_id, name, gender, score) VALUES
  (1, '大宝', 'M', 87),
  (2, '二宝', 'M', 81),
  (3, '三宝', 'M', 83);
-- 查询并观察结果:
SELECT * FROM students;

小结

使用INSERT，我们就可以一次向一个表中插入一条或多条记录。

如果要更新数据库表中的记录，我们就必须使用UPDATE语句。

UPDATE语句的基本语法是：

1	UPDATE <表名> SET 字段1=值1, 字段2=值2, ... WHERE ...;

例如，我们想更新students表id=1的记录的name和score这两个字段，先写出UPDATE students SET name='大牛', score=66，然后在WHERE子句中写出需要更新的行的筛选条件id=1：

-- 更新id=1的记录:
UPDATE students SET name='大牛', score=66 WHERE id=1;
-- 查询并观察结果:
SELECT * FROM students WHERE id=1;

注意到UPDATE语句的WHERE条件和SELECT语句的WHERE条件其实是一样的，因此完全可以一次更新多条记录：

-- 更新id=5,6,7的记录:
UPDATE students SET name='小牛', score=77 WHERE id>=5 AND id<=7;
-- 查询并观察结果:
SELECT * FROM students;

在UPDATE语句中，更新字段时可以使用表达式。例如，把所有80分以下的同学的成绩加10分：

-- 更新score<80的记录:
UPDATE students SET score=score+10 WHERE score<80;
-- 查询并观察结果:
SELECT * FROM students;

其中，SET score=score+10就是给当前行的score字段的值加上了10。

如果WHERE条件没有匹配到任何记录，UPDATE语句不会报错，也不会有任何记录被更新。例如：

-- 更新id=999的记录:
UPDATE students SET score=100 WHERE id=999;
-- 查询并观察结果:
SELECT * FROM students;

最后，要特别小心的是，UPDATE语句可以没有WHERE条件，例如：

1	UPDATE students SET score=60;

这时，整个表的所有记录都会被更新。所以，在执行UPDATE语句时要非常小心，最好先用SELECT语句来测试WHERE条件是否筛选出了期望的记录集，然后再用UPDATE更新。

MySQL

在使用MySQL这类真正的关系数据库时，UPDATE语句会返回更新的行数以及WHERE条件匹配的行数。

例如，更新id=1的记录时：

1
2
3

mysql> UPDATE students SET name='大宝' WHERE id=1;
Query OK, 1 row affected (0.00 sec)
Rows matched: 1  Changed: 1  Warnings: 0

MySQL会返回1，可以从打印的结果Rows matched: 1 Changed: 1看到。

当更新id=999的记录时：

1
2
3

mysql> UPDATE students SET name='大宝' WHERE id=999;
Query OK, 0 rows affected (0.00 sec)
Rows matched: 0  Changed: 0  Warnings: 0

MySQL会返回0，可以从打印的结果Rows matched: 0 Changed: 0看到。

小结

使用UPDATE，我们就可以一次更新表中的一条或多条记录。

删除数据

如果要删除数据库表中的记录，我们可以使用DELETE语句。

DELETE语句的基本语法是：

1	DELETE FROM <表名> WHERE ...;

例如，我们想删除students表中id=1的记录，就需要这么写：

-- 删除id=1的记录:
DELETE FROM students WHERE id=1;
-- 查询并观察结果:
SELECT * FROM students;

注意到DELETE语句的WHERE条件也是用来筛选需要删除的行，因此和UPDATE类似，DELETE语句也可以一次删除多条记录：

-- 删除id=5,6,7的记录:
DELETE FROM students WHERE id>=5 AND id<=7;
-- 查询并观察结果:
SELECT * FROM students;

如果WHERE条件没有匹配到任何记录，DELETE语句不会报错，也不会有任何记录被删除。例如：

-- 删除id=999的记录:
DELETE FROM students WHERE id=999;
-- 查询并观察结果:
SELECT * FROM students;

最后，要特别小心的是，和UPDATE类似，不带WHERE条件的DELETE语句会删除整个表的数据：

1	DELETE FROM students;

这时，整个表的所有记录都会被删除。所以，在执行DELETE语句时也要非常小心，最好先用SELECT语句来测试WHERE条件是否筛选出了期望的记录集，然后再用DELETE删除。

MySQL

在使用MySQL这类真正的关系数据库时，DELETE语句也会返回删除的行数以及WHERE条件匹配的行数。

例如，分别执行删除id=1和id=999的记录：

mysql> DELETE FROM students WHERE id=1;
Query OK, 1 row affected (0.01 sec)

mysql> DELETE FROM students WHERE id=999;
Query OK, 0 rows affected (0.01 sec)

小结

使用DELETE，我们就可以一次删除表中的一条或多条记录。

MySQL

安装完MySQL后，除了MySQL Server，即真正的MySQL服务器外，还附赠一个MySQL Client程序。MySQL Client是一个命令行客户端，可以通过MySQL Client登录MySQL，然后，输入SQL语句并执行。

打开命令提示符，输入命令mysql -u root -p，提示输入口令。填入MySQL的root口令，如果正确，就连上了MySQL Server，同时提示符变为mysql>：

┌─────────────────────────────────────────────────────────┐
│Windows PowerShell                                 - □ x │
├─────────────────────────────────────────────────────────┤
│Windows PowerShell                                       │
│Copyright (C) Microsoft Corporation. All rights reserved.│
│                                                         │
│PS C:\Users\chankein> mysql -u root -p                │
│Enter password: ******                                   │
│                                                         │
│Server version: 5.7                                      │
│Copyright (c) 2000, 2018, ...                            │
│Type 'help;' or '\h' for help.                           │
│                                                         │
│mysql>                                                   │
│                                                         │
└─────────────────────────────────────────────────────────┘

输入exit断开与MySQL Server的连接并返回到命令提示符。

提示

MySQL Client的可执行程序是mysql，MySQL Server的可执行程序是mysqld。

MySQL Client和MySQL Server的关系如下：

1
2
3

┌──────────────┐  SQL   ┌──────────────┐
│ MySQL Client │───────▶│ MySQL Server │
└──────────────┘  TCP   └──────────────┘

在MySQL Client中输入的SQL语句通过TCP连接发送到MySQL Server。默认端口号是3306，即如果发送到本机MySQL Server，地址就是127.0.0.1:3306。

也可以只安装MySQL Client，然后连接到远程MySQL Server。假设远程MySQL Server的IP地址是10.0.1.99，那么就使用-h指定IP或域名：

1	mysql -h 10.0.1.99 -u root -p

小结

命令行程序mysql实际上是MySQL客户端，真正的MySQL服务器程序是mysqld，在后台运行。

要管理MySQL，可以使用可视化图形界面MySQL Workbench。

MySQL Workbench可以用可视化的方式查询、创建和修改数据库表，但是，归根到底，MySQL Workbench是一个图形客户端，它对MySQL的操作仍然是发送SQL语句并执行。因此，本质上，MySQL Workbench和MySQL Client命令行都是客户端，和MySQL交互，唯一的接口就是SQL。

因此，MySQL提供了大量的SQL语句用于管理。虽然可以使用MySQL Workbench图形界面来直接管理MySQL，但是，很多时候，通过SSH远程连接时，只能使用SQL命令，所以，了解并掌握常用的SQL管理操作是必须的。

数据库

在一个运行MySQL的服务器上，实际上可以创建多个数据库（Database）。要列出所有数据库，使用命令：

mysql> SHOW DATABASES;
+--------------------+
| Database           |
+--------------------+
| information_schema |
| mysql              |
| performance_schema |
| shici              |
| sys                |
| test               |
| school             |
+--------------------+

其中，information_schema、mysql、performance_schema和sys是系统库，不要去改动它们。其他的是用户创建的数据库。

注意：在MySQL命令行客户端输入SQL后，记得加一个;表示SQL语句结束，再回车就可以执行该SQL语句。虽然有些SQL命令不需要;也能执行，但类似SELECT等语句不加;会让MySQL客户端换行后继续等待输入。如果在图形界面或程序开发中集成SQL则不需要加;。

要创建一个新数据库，使用命令：

1 2	mysql> CREATE DATABASE test; Query OK, 1 row affected (0.01 sec)

要删除一个数据库，使用命令：

1 2	mysql> DROP DATABASE test; Query OK, 0 rows affected (0.01 sec)

注意：删除一个数据库将导致该数据库的所有表全部被删除。

对一个数据库进行操作时，要首先将其切换为当前数据库：

1 2	mysql> USE test; Database changed

表

列出当前数据库的所有表，使用命令：

mysql> SHOW TABLES;
+---------------------+
| Tables_in_test      |
+---------------------+
| classes             |
| statistics          |
| students            |
| students_of_class1  |
+---------------------+

要查看一个表的结构，使用命令：

mysql> DESC students;
+----------+--------------+------+-----+---------+----------------+
| Field    | Type         | Null | Key | Default | Extra          |
+----------+--------------+------+-----+---------+----------------+
| id       | bigint(20)   | NO   | PRI | NULL    | auto_increment |
| class_id | bigint(20)   | NO   |     | NULL    |                |
| name     | varchar(100) | NO   |     | NULL    |                |
| gender   | varchar(1)   | NO   |     | NULL    |                |
| score    | int(11)      | NO   |     | NULL    |                |
+----------+--------------+------+-----+---------+----------------+
5 rows in set (0.00 sec)

还可以使用以下命令查看创建表的SQL语句：

mysql> SHOW CREATE TABLE students;
+----------+-------------------------------------------------------+
| students | CREATE TABLE `students` (                             |
|          |   `id` bigint(20) NOT NULL AUTO_INCREMENT,            |
|          |   `class_id` bigint(20) NOT NULL,                     |
|          |   `name` varchar(100) NOT NULL,                       |
|          |   `gender` varchar(1) NOT NULL,                       |
|          |   `score` int(11) NOT NULL,                           |
|          |   PRIMARY KEY (`id`)                                  |
|          | ) ENGINE=InnoDB AUTO_INCREMENT=1 DEFAULT CHARSET=utf8 |
+----------+-------------------------------------------------------+
1 row in set (0.00 sec)

创建表使用CREATE TABLE语句，而删除表使用DROP TABLE语句：

1 2	mysql> DROP TABLE students; Query OK, 0 rows affected (0.01 sec)

修改表就比较复杂。如果要给students表新增一列birth，使用：

1	ALTER TABLE students ADD COLUMN birth VARCHAR(10) NOT NULL;

要修改birth列，例如把列名改为birthday，类型改为VARCHAR(20)：

1	ALTER TABLE students CHANGE COLUMN birth birthday VARCHAR(20) NOT NULL;

要删除列，使用：

1	ALTER TABLE students DROP COLUMN birthday;

退出MySQL

使用EXIT命令退出MySQL：

1 2	mysql> EXIT Bye

注意EXIT仅仅断开了客户端和服务器的连接，MySQL服务器仍然继续运行。

在编写SQL时，灵活运用一些技巧，可以大大简化程序逻辑。

插入或替换

如果我们希望插入一条新记录（INSERT），但如果记录已经存在，就先删除原记录，再插入新记录。此时，可以使用REPLACE语句，这样就不必先查询，再决定是否先删除再插入：

1	REPLACE INTO students (id, class_id, name, gender, score) VALUES (1, 1, '小明', 'F', 99);

若id=1的记录不存在，REPLACE语句将插入新记录，否则，当前id=1的记录将被删除，然后再插入新记录。

插入或更新

如果我们希望插入一条新记录（INSERT），但如果记录已经存在，就更新该记录，此时，可以使用INSERT INTO ... ON DUPLICATE KEY UPDATE ...语句：

1	INSERT INTO students (id, class_id, name, gender, score) VALUES (1, 1, '小明', 'F', 99) ON DUPLICATE KEY UPDATE name='小明', gender='F', score=99;

若id=1的记录不存在，INSERT语句将插入新记录，否则，当前id=1的记录将被更新，更新的字段由UPDATE指定。

插入或忽略

如果我们希望插入一条新记录（INSERT），但如果记录已经存在，就啥事也不干直接忽略，此时，可以使用INSERT IGNORE INTO ...语句：

1	INSERT IGNORE INTO students (id, class_id, name, gender, score) VALUES (1, 1, '小明', 'F', 99);

若id=1的记录不存在，INSERT语句将插入新记录，否则，不执行任何操作。

快照

如果想要对一个表进行快照，即复制一份当前表的数据到一个新表，可以结合CREATE TABLE和SELECT：

1 2	-- 对class_id=1的记录进行快照，并存储为新表students_of_class1: CREATE TABLE students_of_class1 SELECT * FROM students WHERE class_id=1;

新创建的表结构和SELECT使用的表结构完全一致。

写入查询结果集

如果查询结果集需要写入到表中，可以结合INSERT和SELECT，将SELECT语句的结果集直接插入到指定表中。

例如，创建一个统计成绩的表statistics，记录各班的平均成绩：

CREATE TABLE statistics (
    id BIGINT NOT NULL AUTO_INCREMENT,
    class_id BIGINT NOT NULL,
    average DOUBLE NOT NULL,
    PRIMARY KEY (id)
);

然后，我们就可以用一条语句写入各班的平均成绩：

1	INSERT INTO statistics (class_id, average) SELECT class_id, AVG(score) FROM students GROUP BY class_id;

确保INSERT语句的列和SELECT语句的列能一一对应，就可以在statistics表中直接保存查询的结果：

> SELECT * FROM statistics;
+----+----------+--------------+
| id | class_id | average      |
+----+----------+--------------+
|  1 |        1 |         86.5 |
|  2 |        2 | 73.666666666 |
|  3 |        3 | 88.333333333 |
+----+----------+--------------+
3 rows in set (0.00 sec)

强制使用指定索引

在查询的时候，数据库系统会自动分析查询语句，并选择一个最合适的索引。但是很多时候，数据库系统的查询优化器并不一定总是能使用最优索引。如果我们知道如何选择索引，可以使用FORCE INDEX强制查询使用指定的索引。例如：

1	SELECT * FROM students FORCE INDEX (idx_class_id) WHERE class_id = 1 ORDER BY id DESC;

指定索引的前提是索引idx_class_id必须存在。

事务

在执行SQL语句的时候，某些业务要求，一系列操作必须全部执行，而不能仅执行一部分。例如，一个转账操作：

-- 从id=1的账户给id=2的账户转账100元
-- 第一步：将id=1的A账户余额减去100
UPDATE accounts SET balance = balance - 100 WHERE id = 1;
-- 第二步：将id=2的B账户余额加上100
UPDATE accounts SET balance = balance + 100 WHERE id = 2;

这两条SQL语句必须全部执行，或者，由于某些原因，如果第一条语句成功，第二条语句失败，就必须全部撤销。

这种把多条语句作为一个整体进行操作的功能，被称为数据库事务。数据库事务可以确保该事务范围内的所有操作都可以全部成功或者全部失败。如果事务失败，那么效果就和没有执行这些SQL一样，不会对数据库数据有任何改动。

可见，数据库事务具有ACID这4个特性：

A：Atomicity，原子性，将所有SQL作为原子工作单元执行，要么全部执行，要么全部不执行；
C：Consistency，一致性，事务完成后，所有数据的状态都是一致的，即A账户只要减去了100，B账户则必定加上了100；
I：Isolation，隔离性，如果有多个事务并发执行，每个事务作出的修改必须与其他事务隔离；
D：Durability，持久性，即事务完成后，对数据库数据的修改被持久化存储。

对于单条SQL语句，数据库系统自动将其作为一个事务执行，这种事务被称为隐式事务。

要手动把多条SQL语句作为一个事务执行，使用BEGIN开启一个事务，使用COMMIT提交一个事务，这种事务被称为显式事务，例如，把上述的转账操作作为一个显式事务：

BEGIN;
UPDATE accounts SET balance = balance - 100 WHERE id = 1;
UPDATE accounts SET balance = balance + 100 WHERE id = 2;
COMMIT;

很显然多条SQL语句要想作为一个事务执行，就必须使用显式事务。

COMMIT是指提交事务，即试图把事务内的所有SQL所做的修改永久保存。如果COMMIT语句执行失败了，整个事务也会失败。

有些时候，我们希望主动让事务失败，这时，可以用ROLLBACK回滚事务，整个事务会失败：

BEGIN;
UPDATE accounts SET balance = balance - 100 WHERE id = 1;
UPDATE accounts SET balance = balance + 100 WHERE id = 2;
ROLLBACK;

数据库事务是由数据库系统保证的，我们只需要根据业务逻辑使用它就可以。

隔离级别

对于两个并发执行的事务，如果涉及到操作同一条记录的时候，可能会发生问题。因为并发操作会带来数据的不一致性，包括脏读、不可重复读、幻读等。数据库系统提供了隔离级别来让我们有针对性地选择事务的隔离级别，避免数据不一致的问题。

SQL标准定义了4种隔离级别，分别对应可能出现的数据不一致的情况：

Isolation Level	脏读（Dirty Read）	不可重复读（Non Repeatable Read）	幻读（Phantom Read）
Read Uncommitted	Yes	Yes	Yes
Read Committed	-	Yes	Yes
Repeatable Read	-	-	Yes
Serializable	-	-	-

我们会依次介绍4种隔离级别的数据一致性问题。

小结

数据库事务具有ACID特性，用来保证多条SQL的全部执行。

Read Uncommitted

Read Uncommitted是隔离级别最低的一种事务级别。在这种隔离级别下，一个事务会读到另一个事务更新后但未提交的数据，如果另一个事务回滚，那么当前事务读到的数据就是脏数据，这就是脏读（Dirty Read）。

我们来看一个例子。

首先，我们准备好students表的数据，该表仅一行记录：

mysql> select * from students;
+----+-------+
| id | name  |
+----+-------+
|  1 | Alice |
+----+-------+
1 row in set (0.00 sec)

然后，分别开启两个MySQL客户端连接，按顺序依次执行事务A和事务B：

时刻	事务A	事务B
1	SET TRANSACTION ISOLATION LEVEL READ UNCOMMITTED;	SET TRANSACTION ISOLATION LEVEL READ UNCOMMITTED;
2	BEGIN;	BEGIN;
3	UPDATE students SET name = ‘Bob’ WHERE id = 1;
4		SELECT * FROM students WHERE id = 1;
5	ROLLBACK;
6		SELECT * FROM students WHERE id = 1;
7		COMMIT;

当事务A执行完第3步时，它更新了id=1的记录，但并未提交，而事务B在第4步读取到的数据就是未提交的数据。

随后，事务A在第5步进行了回滚，事务B再次读取id=1的记录，发现和上一次读取到的数据不一致，这就是脏读。

可见，在Read Uncommitted隔离级别下，一个事务可能读取到另一个事务更新但未提交的数据，这个数据有可能是脏数据。

Read Committed

在Read Committed隔离级别下，一个事务不会读到另一个事务还没有提交的数据，但可能会遇到不可重复读（Non Repeatable Read）的问题。

不可重复读是指，在一个事务内，多次读同一数据，在这个事务还没有结束时，如果另一个事务恰好修改了这个数据，那么，在第一个事务中，两次读取的数据就可能不一致。

我们仍然先准备好students表的数据：

mysql> select * from students;
+----+-------+
| id | name  |
+----+-------+
|  1 | Alice |
+----+-------+
1 row in set (0.00 sec)

然后，分别开启两个MySQL客户端连接，按顺序依次执行事务A和事务B：

时刻	事务A	事务B
1	SET TRANSACTION ISOLATION LEVEL READ COMMITTED;	SET TRANSACTION ISOLATION LEVEL READ COMMITTED;
2	BEGIN;	BEGIN;
3		SELECT * FROM students WHERE id = 1; – Alice
4	UPDATE students SET name = ‘Bob’ WHERE id = 1;
5	COMMIT;
6		SELECT * FROM students WHERE id = 1; – Bob
7		COMMIT;

当事务B第一次执行第3步的查询时，得到的结果是Alice，随后，由于事务A在第4步更新了这条记录并提交，所以，事务B在第6步再次执行同样的查询时，得到的结果就变成了Bob，因此，在Read Committed隔离级别下，事务不可重复读同一条记录，因为很可能读到的结果不一致。

Repeatable Read

在Repeatable Read隔离级别下，一个事务可能会遇到幻读（Phantom Read）的问题。

幻读是指，在一个事务中，第一次查询某条记录，发现没有，但是，当试图更新这条不存在的记录时，竟然能成功，并且，再次读取同一条记录，它就神奇地出现了。

我们仍然先准备好students表的数据：

mysql> select * from students;
+----+-------+
| id | name  |
+----+-------+
|  1 | Alice |
+----+-------+
1 row in set (0.00 sec)

然后，分别开启两个MySQL客户端连接，按顺序依次执行事务A和事务B：

时刻	事务A	事务B
1	SET TRANSACTION ISOLATION LEVEL REPEATABLE READ;	SET TRANSACTION ISOLATION LEVEL REPEATABLE READ;
2	BEGIN;	BEGIN;
3		SELECT * FROM students WHERE id = 99; – empty
4	INSERT INTO students (id, name) VALUES (99, ‘Bob’);
5	COMMIT;
6		SELECT * FROM students WHERE id = 99; – empty
7		UPDATE students SET name = ‘Alice’ WHERE id = 99; – 1 row affected
8		SELECT * FROM students WHERE id = 99; – Alice
9		COMMIT;

事务B在第3步第一次读取id=99的记录时，读到的记录为空，说明不存在id=99的记录。随后，事务A在第4步插入了一条id=99的记录并提交。事务B在第6步再次读取id=99的记录时，读到的记录仍然为空，但是，事务B在第7步试图更新这条不存在的记录时，竟然成功了，并且，事务B在第8步再次读取id=99的记录时，记录出现了。

可见，幻读就是没有读到的记录，以为不存在，但其实是可以更新成功的，并且，更新成功后，再次读取，就出现了。

Serializable是最严格的隔离级别。在Serializable隔离级别下，所有事务按照次序依次执行，因此，脏读、不可重复读、幻读都不会出现。

虽然Serializable隔离级别下的事务具有最高的安全性，但是，由于事务是串行执行，所以效率会大大下降，应用程序的性能会急剧降低。如果没有特别重要的情景，一般都不会使用Serializable隔离级别。

默认隔离级别

如果没有指定隔离级别，数据库就会使用默认的隔离级别。在MySQL中，如果使用InnoDB，默认的隔离级别是Repeatable Read。

留言與分享

pandas 快速入门

2015 年 6 月 16 日分類 database, pandas

pandas 快速入门#

这是 pandas 的一个简短介绍，主要面向新用户。你可以在实用代码片段中查看更复杂的示例。

通常，我们按如下方式导入

1
2
3

In [1]: import numpy as np

In [2]: import pandas as pd

pandas 中的基本数据结构#

Pandas 提供了两种用于处理数据的类

Series：一个一维的带标签数组，可容纳任何类型的数据

例如整数、字符串、Python 对象等。
DataFrame：一个二维数据结构，像二维数组或带有行和列的表格一样容纳数据。

对象创建#

请参阅数据结构简介部分。

通过传入值列表创建Series，让 pandas 创建默认的RangeIndex。

In [3]: s = pd.Series([1, 3, 5, np.nan, 6, 8])

In [4]: s
Out[4]: 
0    1.0
1    3.0
2    5.0
3    NaN
4    6.0
5    8.0
dtype: float64

通过传入 NumPy 数组，使用date_range()创建带有日期时间索引和标签列的DataFrame

In [5]: dates = pd.date_range("20130101", periods=6)

In [6]: dates
Out[6]: 
DatetimeIndex(['2013-01-01', '2013-01-02', '2013-01-03', '2013-01-04',
               '2013-01-05', '2013-01-06'],
              dtype='datetime64[ns]', freq='D')

In [7]: df = pd.DataFrame(np.random.randn(6, 4), index=dates, columns=list("ABCD"))

In [8]: df
Out[8]: 
                   A         B         C         D
2013-01-01  0.469112 -0.282863 -1.509059 -1.135632
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804
2013-01-04  0.721555 -0.706771 -1.039575  0.271860
2013-01-05 -0.424972  0.567020  0.276232 -1.087401
2013-01-06 -0.673690  0.113648 -1.478427  0.524988

通过传入一个对象字典创建DataFrame，其中键是列标签，值是列值。

In [9]: df2 = pd.DataFrame(
   ...:     {
   ...:         "A": 1.0,
   ...:         "B": pd.Timestamp("20130102"),
   ...:         "C": pd.Series(1, index=list(range(4)), dtype="float32"),
   ...:         "D": np.array([3] * 4, dtype="int32"),
   ...:         "E": pd.Categorical(["test", "train", "test", "train"]),
   ...:         "F": "foo",
   ...:     }
   ...: )
   ...: 

In [10]: df2
Out[10]: 
     A          B    C  D      E    F
0  1.0 2013-01-02  1.0  3   test  foo
1  1.0 2013-01-02  1.0  3  train  foo
2  1.0 2013-01-02  1.0  3   test  foo
3  1.0 2013-01-02  1.0  3  train  foo

生成的DataFrame的列具有不同的dtypes

In [11]: df2.dtypes
Out[11]: 
A          float64
B    datetime64[s]
C          float32
D            int32
E         category
F           object
dtype: object

如果你使用 IPython，列名（以及公共属性）的 Tab 自动补全功能会自动启用。以下是部分将自动补全的属性：

In [12]: df2.<TAB>  # noqa: E225, E999
df2.A                  df2.bool
df2.abs                df2.boxplot
df2.add                df2.C
df2.add_prefix         df2.clip
df2.add_suffix         df2.columns
df2.align              df2.copy
df2.all                df2.count
df2.any                df2.combine
df2.append             df2.D
df2.apply              df2.describe
df2.applymap           df2.diff
df2.B                  df2.duplicated

如你所见，列 A、B、C 和 D 会自动 Tab 补全。E 和 F 也在其中；其余属性为简洁起见已被截断。

查看数据#

请参阅基本核心功能部分。

使用DataFrame.head()和DataFrame.tail()分别查看框架的顶部和底部行。

In [13]: df.head()
Out[13]: 
                   A         B         C         D
2013-01-01  0.469112 -0.282863 -1.509059 -1.135632
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804
2013-01-04  0.721555 -0.706771 -1.039575  0.271860
2013-01-05 -0.424972  0.567020  0.276232 -1.087401

In [14]: df.tail(3)
Out[14]: 
                   A         B         C         D
2013-01-04  0.721555 -0.706771 -1.039575  0.271860
2013-01-05 -0.424972  0.567020  0.276232 -1.087401
2013-01-06 -0.673690  0.113648 -1.478427  0.524988

显示DataFrame.index或DataFrame.columns

In [15]: df.index
Out[15]: 
DatetimeIndex(['2013-01-01', '2013-01-02', '2013-01-03', '2013-01-04',
               '2013-01-05', '2013-01-06'],
              dtype='datetime64[ns]', freq='D')

In [16]: df.columns
Out[16]: Index(['A', 'B', 'C', 'D'], dtype='object')

使用DataFrame.to_numpy()返回底层数据的 NumPy 表示，不包含索引或列标签。

In [17]: df.to_numpy()
Out[17]: 
array([[ 0.4691, -0.2829, -1.5091, -1.1356],
       [ 1.2121, -0.1732,  0.1192, -1.0442],
       [-0.8618, -2.1046, -0.4949,  1.0718],
       [ 0.7216, -0.7068, -1.0396,  0.2719],
       [-0.425 ,  0.567 ,  0.2762, -1.0874],
       [-0.6737,  0.1136, -1.4784,  0.525 ]])

注意

NumPy 数组的整个数组只有一个 dtype，而 pandas DataFrames 的每列有一个 dtype。当你调用DataFrame.to_numpy()时，pandas 会找到能够容纳 DataFrame 中所有 dtypes 的 NumPy dtype。如果共同的数据类型是 object，则DataFrame.to_numpy()将需要复制数据。

In [18]: df2.dtypes
Out[18]: 
A          float64
B    datetime64[s]
C          float32
D            int32
E         category
F           object
dtype: object

In [19]: df2.to_numpy()
Out[19]: 
array([[1.0, Timestamp('2013-01-02 00:00:00'), 1.0, 3, 'test', 'foo'],
       [1.0, Timestamp('2013-01-02 00:00:00'), 1.0, 3, 'train', 'foo'],
       [1.0, Timestamp('2013-01-02 00:00:00'), 1.0, 3, 'test', 'foo'],
       [1.0, Timestamp('2013-01-02 00:00:00'), 1.0, 3, 'train', 'foo']],
      dtype=object)

describe()显示数据的快速统计摘要

In [20]: df.describe()
Out[20]: 
              A         B         C         D
count  6.000000  6.000000  6.000000  6.000000
mean   0.073711 -0.431125 -0.687758 -0.233103
std    0.843157  0.922818  0.779887  0.973118
min   -0.861849 -2.104569 -1.509059 -1.135632
25%   -0.611510 -0.600794 -1.368714 -1.076610
50%    0.022070 -0.228039 -0.767252 -0.386188
75%    0.658444  0.041933 -0.034326  0.461706
max    1.212112  0.567020  0.276232  1.071804

转置数据

In [21]: df.T
Out[21]: 
   2013-01-01  2013-01-02  2013-01-03  2013-01-04  2013-01-05  2013-01-06
A    0.469112    1.212112   -0.861849    0.721555   -0.424972   -0.673690
B   -0.282863   -0.173215   -2.104569   -0.706771    0.567020    0.113648
C   -1.509059    0.119209   -0.494929   -1.039575    0.276232   -1.478427
D   -1.135632   -1.044236    1.071804    0.271860   -1.087401    0.524988

DataFrame.sort_index()按轴排序

In [22]: df.sort_index(axis=1, ascending=False)
Out[22]: 
                   D         C         B         A
2013-01-01 -1.135632 -1.509059 -0.282863  0.469112
2013-01-02 -1.044236  0.119209 -0.173215  1.212112
2013-01-03  1.071804 -0.494929 -2.104569 -0.861849
2013-01-04  0.271860 -1.039575 -0.706771  0.721555
2013-01-05 -1.087401  0.276232  0.567020 -0.424972
2013-01-06  0.524988 -1.478427  0.113648 -0.673690

DataFrame.sort_values()按值排序

In [23]: df.sort_values(by="B")
Out[23]: 
                   A         B         C         D
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804
2013-01-04  0.721555 -0.706771 -1.039575  0.271860
2013-01-01  0.469112 -0.282863 -1.509059 -1.135632
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-06 -0.673690  0.113648 -1.478427  0.524988
2013-01-05 -0.424972  0.567020  0.276232 -1.087401

选择#

请参阅索引文档索引与选择数据和MultiIndex / 高级索引。

Getitem (`[]`)#

对于DataFrame，传入单个标签会选择一列并生成一个Series，等同于 df.A

In [24]: df["A"]
Out[24]: 
2013-01-01    0.469112
2013-01-02    1.212112
2013-01-03   -0.861849
2013-01-04    0.721555
2013-01-05   -0.424972
2013-01-06   -0.673690
Freq: D, Name: A, dtype: float64

对于DataFrame，传入切片 : 会选择匹配的行。

In [25]: df[0:3]
Out[25]: 
                   A         B         C         D
2013-01-01  0.469112 -0.282863 -1.509059 -1.135632
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804

In [26]: df["20130102":"20130104"]
Out[26]: 
                   A         B         C         D
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804
2013-01-04  0.721555 -0.706771 -1.039575  0.271860

按标签选择#

更多信息请参阅按标签选择，使用DataFrame.loc()或DataFrame.at()。

选择与标签匹配的行

In [27]: df.loc[dates[0]]
Out[27]: 
A    0.469112
B   -0.282863
C   -1.509059
D   -1.135632
Name: 2013-01-01 00:00:00, dtype: float64

选择所有行 (:) 和选定的列标签

In [28]: df.loc[:, ["A", "B"]]
Out[28]: 
                   A         B
2013-01-01  0.469112 -0.282863
2013-01-02  1.212112 -0.173215
2013-01-03 -0.861849 -2.104569
2013-01-04  0.721555 -0.706771
2013-01-05 -0.424972  0.567020
2013-01-06 -0.673690  0.113648

对于标签切片，两个端点都包含在内

In [29]: df.loc["20130102":"20130104", ["A", "B"]]
Out[29]: 
                   A         B
2013-01-02  1.212112 -0.173215
2013-01-03 -0.861849 -2.104569
2013-01-04  0.721555 -0.706771

选择单个行和列标签会返回一个标量

1 2	In [30]: df.loc[dates[0], "A"] Out[30]: 0.4691122999071863

为了快速访问标量（等同于之前的方法）

1 2	In [31]: df.at[dates[0], "A"] Out[31]: 0.4691122999071863

按位置选择#

更多信息请参阅按位置选择，使用DataFrame.iloc()或DataFrame.iat()。

通过传入整数的位置进行选择

In [32]: df.iloc[3]
Out[32]: 
A    0.721555
B   -0.706771
C   -1.039575
D    0.271860
Name: 2013-01-04 00:00:00, dtype: float64

整数切片行为类似于 NumPy/Python

In [33]: df.iloc[3:5, 0:2]
Out[33]: 
                   A         B
2013-01-04  0.721555 -0.706771
2013-01-05 -0.424972  0.567020

整数位置列表

In [34]: df.iloc[[1, 2, 4], [0, 2]]
Out[34]: 
                   A         C
2013-01-02  1.212112  0.119209
2013-01-03 -0.861849 -0.494929
2013-01-05 -0.424972  0.276232

显式切片行

In [35]: df.iloc[1:3, :]
Out[35]: 
                   A         B         C         D
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804

显式切片列

In [36]: df.iloc[:, 1:3]
Out[36]: 
                   B         C
2013-01-01 -0.282863 -1.509059
2013-01-02 -0.173215  0.119209
2013-01-03 -2.104569 -0.494929
2013-01-04 -0.706771 -1.039575
2013-01-05  0.567020  0.276232
2013-01-06  0.113648 -1.478427

显式获取值

1 2	In [37]: df.iloc[1, 1] Out[37]: -0.17321464905330858

为了快速访问标量（等同于之前的方法）

1 2	In [38]: df.iat[1, 1] Out[38]: -0.17321464905330858

布尔索引#

选择 df.A 大于 0 的行。

In [39]: df[df["A"] > 0]
Out[39]: 
                   A         B         C         D
2013-01-01  0.469112 -0.282863 -1.509059 -1.135632
2013-01-02  1.212112 -0.173215  0.119209 -1.044236
2013-01-04  0.721555 -0.706771 -1.039575  0.271860

从满足布尔条件的DataFrame中选择值

In [40]: df[df > 0]
Out[40]: 
                   A         B         C         D
2013-01-01  0.469112       NaN       NaN       NaN
2013-01-02  1.212112       NaN  0.119209       NaN
2013-01-03       NaN       NaN       NaN  1.071804
2013-01-04  0.721555       NaN       NaN  0.271860
2013-01-05       NaN  0.567020  0.276232       NaN
2013-01-06       NaN  0.113648       NaN  0.524988

使用isin()方法进行过滤

In [41]: df2 = df.copy()

In [42]: df2["E"] = ["one", "one", "two", "three", "four", "three"]

In [43]: df2
Out[43]: 
                   A         B         C         D      E
2013-01-01  0.469112 -0.282863 -1.509059 -1.135632    one
2013-01-02  1.212112 -0.173215  0.119209 -1.044236    one
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804    two
2013-01-04  0.721555 -0.706771 -1.039575  0.271860  three
2013-01-05 -0.424972  0.567020  0.276232 -1.087401   four
2013-01-06 -0.673690  0.113648 -1.478427  0.524988  three

In [44]: df2[df2["E"].isin(["two", "four"])]
Out[44]: 
                   A         B         C         D     E
2013-01-03 -0.861849 -2.104569 -0.494929  1.071804   two
2013-01-05 -0.424972  0.567020  0.276232 -1.087401  four

设置#

设置新列会自动按索引对齐数据

In [45]: s1 = pd.Series([1, 2, 3, 4, 5, 6], index=pd.date_range("20130102", periods=6))

In [46]: s1
Out[46]: 
2013-01-02    1
2013-01-03    2
2013-01-04    3
2013-01-05    4
2013-01-06    5
2013-01-07    6
Freq: D, dtype: int64

In [47]: df["F"] = s1

按标签设置值

1	In [48]: df.at[dates[0], "A"] = 0

按位置设置值

1	In [49]: df.iat[0, 1] = 0

通过分配 NumPy 数组进行设置

1	In [50]: df.loc[:, "D"] = np.array([5] * len(df))

先前的设置操作的结果

In [51]: df
Out[51]: 
                   A         B         C    D    F
2013-01-01  0.000000  0.000000 -1.509059  5.0  NaN
2013-01-02  1.212112 -0.173215  0.119209  5.0  1.0
2013-01-03 -0.861849 -2.104569 -0.494929  5.0  2.0
2013-01-04  0.721555 -0.706771 -1.039575  5.0  3.0
2013-01-05 -0.424972  0.567020  0.276232  5.0  4.0
2013-01-06 -0.673690  0.113648 -1.478427  5.0  5.0

带设置的 where 操作

In [52]: df2 = df.copy()

In [53]: df2[df2 > 0] = -df2

In [54]: df2
Out[54]: 
                   A         B         C    D    F
2013-01-01  0.000000  0.000000 -1.509059 -5.0  NaN
2013-01-02 -1.212112 -0.173215 -0.119209 -5.0 -1.0
2013-01-03 -0.861849 -2.104569 -0.494929 -5.0 -2.0
2013-01-04 -0.721555 -0.706771 -1.039575 -5.0 -3.0
2013-01-05 -0.424972 -0.567020 -0.276232 -5.0 -4.0
2013-01-06 -0.673690 -0.113648 -1.478427 -5.0 -5.0

缺失数据#

对于 NumPy 数据类型，np.nan 表示缺失数据。默认情况下，它不包含在计算中。请参阅缺失数据部分。

重新索引允许你更改/添加/删除指定轴上的索引。这会返回数据的副本。

In [55]: df1 = df.reindex(index=dates[0:4], columns=list(df.columns) + ["E"])

In [56]: df1.loc[dates[0] : dates[1], "E"] = 1

In [57]: df1
Out[57]: 
                   A         B         C    D    F    E
2013-01-01  0.000000  0.000000 -1.509059  5.0  NaN  1.0
2013-01-02  1.212112 -0.173215  0.119209  5.0  1.0  1.0
2013-01-03 -0.861849 -2.104569 -0.494929  5.0  2.0  NaN
2013-01-04  0.721555 -0.706771 -1.039575  5.0  3.0  NaN

DataFrame.dropna()删除任何包含缺失数据的行

In [58]: df1.dropna(how="any")
Out[58]: 
                   A         B         C    D    F    E
2013-01-02  1.212112 -0.173215  0.119209  5.0  1.0  1.0

DataFrame.fillna()填充缺失数据

In [59]: df1.fillna(value=5)
Out[59]: 
                   A         B         C    D    F    E
2013-01-01  0.000000  0.000000 -1.509059  5.0  5.0  1.0
2013-01-02  1.212112 -0.173215  0.119209  5.0  1.0  1.0
2013-01-03 -0.861849 -2.104569 -0.494929  5.0  2.0  5.0
2013-01-04  0.721555 -0.706771 -1.039575  5.0  3.0  5.0

isna()获取值为 nan 的布尔掩码

In [60]: pd.isna(df1)
Out[60]: 
                A      B      C      D      F      E
2013-01-01  False  False  False  False   True  False
2013-01-02  False  False  False  False  False  False
2013-01-03  False  False  False  False  False   True
2013-01-04  False  False  False  False  False   True

操作#

请参阅二元运算基本部分。

统计#

操作通常排除缺失数据。

计算每列的平均值

In [61]: df.mean()
Out[61]: 
A   -0.004474
B   -0.383981
C   -0.687758
D    5.000000
F    3.000000
dtype: float64

计算每行的平均值

In [62]: df.mean(axis=1)
Out[62]: 
2013-01-01    0.872735
2013-01-02    1.431621
2013-01-03    0.707731
2013-01-04    1.395042
2013-01-05    1.883656
2013-01-06    1.592306
Freq: D, dtype: float64

与具有不同索引或列的另一个Series或DataFrame进行操作时，结果将与索引或列标签的并集对齐。此外，pandas 会沿指定维度自动广播，并将未对齐的标签填充为np.nan。

In [63]: s = pd.Series([1, 3, 5, np.nan, 6, 8], index=dates).shift(2)

In [64]: s
Out[64]: 
2013-01-01    NaN
2013-01-02    NaN
2013-01-03    1.0
2013-01-04    3.0
2013-01-05    5.0
2013-01-06    NaN
Freq: D, dtype: float64

In [65]: df.sub(s, axis="index")
Out[65]: 
                   A         B         C    D    F
2013-01-01       NaN       NaN       NaN  NaN  NaN
2013-01-02       NaN       NaN       NaN  NaN  NaN
2013-01-03 -1.861849 -3.104569 -1.494929  4.0  1.0
2013-01-04 -2.278445 -3.706771 -4.039575  2.0  0.0
2013-01-05 -5.424972 -4.432980 -4.723768  0.0 -1.0
2013-01-06       NaN       NaN       NaN  NaN  NaN

用户定义函数#

DataFrame.agg()和DataFrame.transform()分别应用一个用户定义函数，该函数会减少或广播其结果。

In [66]: df.agg(lambda x: np.mean(x) * 5.6)
Out[66]: 
A    -0.025054
B    -2.150294
C    -3.851445
D    28.000000
F    16.800000
dtype: float64

In [67]: df.transform(lambda x: x * 101.2)
Out[67]: 
                     A           B           C      D      F
2013-01-01    0.000000    0.000000 -152.716721  506.0    NaN
2013-01-02  122.665737  -17.529322   12.063922  506.0  101.2
2013-01-03  -87.219115 -212.982405  -50.086843  506.0  202.4
2013-01-04   73.021382  -71.525239 -105.204988  506.0  303.6
2013-01-05  -43.007200   57.382459   27.954680  506.0  404.8
2013-01-06  -68.177398   11.501219 -149.616767  506.0  506.0

值计数#

更多信息请参阅直方图和离散化。

In [68]: s = pd.Series(np.random.randint(0, 7, size=10))

In [69]: s
Out[69]: 
0    4
1    2
2    1
3    2
4    6
5    4
6    4
7    6
8    4
9    4
dtype: int64

In [70]: s.value_counts()
Out[70]: 
4    5
2    2
6    2
1    1
Name: count, dtype: int64

字符串方法#

Series在 str 属性中配备了一组字符串处理方法，可以轻松地对数组的每个元素进行操作，如下面的代码片段所示。更多信息请参阅矢量化字符串方法。

In [71]: s = pd.Series(["A", "B", "C", "Aaba", "Baca", np.nan, "CABA", "dog", "cat"])

In [72]: s.str.lower()
Out[72]: 
0       a
1       b
2       c
3    aaba
4    baca
5     NaN
6    caba
7     dog
8     cat
dtype: object

合并#

拼接#

pandas 提供了各种功能，可以轻松地将 Series 和 DataFrame 对象与各种集合逻辑（用于索引）和关系代数功能（用于连接/合并类型操作）结合在一起。

请参阅合并部分。

使用concat()按行拼接 pandas 对象

In [73]: df = pd.DataFrame(np.random.randn(10, 4))

In [74]: df
Out[74]: 
          0         1         2         3
0 -0.548702  1.467327 -1.015962 -0.483075
1  1.637550 -1.217659 -0.291519 -1.745505
2 -0.263952  0.991460 -0.919069  0.266046
3 -0.709661  1.669052  1.037882 -1.705775
4 -0.919854 -0.042379  1.247642 -0.009920
5  0.290213  0.495767  0.362949  1.548106
6 -1.131345 -0.089329  0.337863 -0.945867
7 -0.932132  1.956030  0.017587 -0.016692
8 -0.575247  0.254161 -1.143704  0.215897
9  1.193555 -0.077118 -0.408530 -0.862495

# break it into pieces
In [75]: pieces = [df[:3], df[3:7], df[7:]]

In [76]: pd.concat(pieces)
Out[76]: 
          0         1         2         3
0 -0.548702  1.467327 -1.015962 -0.483075
1  1.637550 -1.217659 -0.291519 -1.745505
2 -0.263952  0.991460 -0.919069  0.266046
3 -0.709661  1.669052  1.037882 -1.705775
4 -0.919854 -0.042379  1.247642 -0.009920
5  0.290213  0.495767  0.362949  1.548106
6 -1.131345 -0.089329  0.337863 -0.945867
7 -0.932132  1.956030  0.017587 -0.016692
8 -0.575247  0.254161 -1.143704  0.215897
9  1.193555 -0.077118 -0.408530 -0.862495

连接#

merge()支持沿着特定列进行 SQL 风格的连接。请参阅数据库风格连接部分。

In [77]: left = pd.DataFrame({"key": ["foo", "foo"], "lval": [1, 2]})

In [78]: right = pd.DataFrame({"key": ["foo", "foo"], "rval": [4, 5]})

In [79]: left
Out[79]: 
   key  lval
0  foo     1
1  foo     2

In [80]: right
Out[80]: 
   key  rval
0  foo     4
1  foo     5

In [81]: pd.merge(left, right, on="key")
Out[81]: 
   key  lval  rval
0  foo     1     4
1  foo     1     5
2  foo     2     4
3  foo     2     5

merge() 基于唯一键进行合并

In [82]: left = pd.DataFrame({"key": ["foo", "bar"], "lval": [1, 2]})

In [83]: right = pd.DataFrame({"key": ["foo", "bar"], "rval": [4, 5]})

In [84]: left
Out[84]: 
   key  lval
0  foo     1
1  bar     2

In [85]: right
Out[85]: 
   key  rval
0  foo     4
1  bar     5

In [86]: pd.merge(left, right, on="key")
Out[86]: 
   key  lval  rval
0  foo     1     4
1  bar     2     5

分组#

“分组”指的是一个或多个以下步骤的过程

根据某些条件将数据分拆成组
对每个组独立地应用一个函数
将结果组合成一个数据结构

请参阅分组部分。

In [87]: df = pd.DataFrame(
   ....:     {
   ....:         "A": ["foo", "bar", "foo", "bar", "foo", "bar", "foo", "foo"],
   ....:         "B": ["one", "one", "two", "three", "two", "two", "one", "three"],
   ....:         "C": np.random.randn(8),
   ....:         "D": np.random.randn(8),
   ....:     }
   ....: )
   ....: 

In [88]: df
Out[88]: 
     A      B         C         D
0  foo    one  1.346061 -1.577585
1  bar    one  1.511763  0.396823
2  foo    two  1.627081 -0.105381
3  bar  three -0.990582 -0.532532
4  foo    two -0.441652  1.453749
5  bar    two  1.211526  1.208843
6  foo    one  0.268520 -0.080952
7  foo  three  0.024580 -0.264610

按列标签分组，选择列标签，然后将DataFrameGroupBy.sum()函数应用于结果组

In [89]: df.groupby("A")[["C", "D"]].sum()
Out[89]: 
            C         D
A                      
bar  1.732707  1.073134
foo  2.824590 -0.574779

按多列标签分组会形成MultiIndex。

In [90]: df.groupby(["A", "B"]).sum()
Out[90]: 
                  C         D
A   B                        
bar one    1.511763  0.396823
    three -0.990582 -0.532532
    two    1.211526  1.208843
foo one    1.614581 -1.658537
    three  0.024580 -0.264610
    two    1.185429  1.348368

重塑#

请参阅层次化索引和重塑部分。

堆叠#

In [91]: arrays = [
   ....:    ["bar", "bar", "baz", "baz", "foo", "foo", "qux", "qux"],
   ....:    ["one", "two", "one", "two", "one", "two", "one", "two"],
   ....: ]
   ....: 

In [92]: index = pd.MultiIndex.from_arrays(arrays, names=["first", "second"])

In [93]: df = pd.DataFrame(np.random.randn(8, 2), index=index, columns=["A", "B"])

In [94]: df2 = df[:4]

In [95]: df2
Out[95]: 
                     A         B
first second                    
bar   one    -0.727965 -0.589346
      two     0.339969 -0.693205
baz   one    -0.339355  0.593616
      two     0.884345  1.591431

stack()方法“压缩”了 DataFrame 列中的一个层

In [96]: stacked = df2.stack(future_stack=True)

In [97]: stacked
Out[97]: 
first  second   
bar    one     A   -0.727965
               B   -0.589346
       two     A    0.339969
               B   -0.693205
baz    one     A   -0.339355
               B    0.593616
       two     A    0.884345
               B    1.591431
dtype: float64

对于一个“堆叠”的 DataFrame 或 Series（其 index 为 MultiIndex），stack() 的逆操作是 unstack()，它默认会解除堆叠最底层

In [98]: stacked.unstack()
Out[98]: 
                     A         B
first second                    
bar   one    -0.727965 -0.589346
      two     0.339969 -0.693205
baz   one    -0.339355  0.593616
      two     0.884345  1.591431

In [99]: stacked.unstack(1)
Out[99]: 
second        one       two
first                      
bar   A -0.727965  0.339969
      B -0.589346 -0.693205
baz   A -0.339355  0.884345
      B  0.593616  1.591431

In [100]: stacked.unstack(0)
Out[100]: 
first          bar       baz
second                      
one    A -0.727965 -0.339355
       B -0.589346  0.593616
two    A  0.339969  0.884345
       B -0.693205  1.591431

透视表#

请参阅透视表部分。

In [101]: df = pd.DataFrame(
   .....:     {
   .....:         "A": ["one", "one", "two", "three"] * 3,
   .....:         "B": ["A", "B", "C"] * 4,
   .....:         "C": ["foo", "foo", "foo", "bar", "bar", "bar"] * 2,
   .....:         "D": np.random.randn(12),
   .....:         "E": np.random.randn(12),
   .....:     }
   .....: )
   .....: 

In [102]: df
Out[102]: 
        A  B    C         D         E
0     one  A  foo -1.202872  0.047609
1     one  B  foo -1.814470 -0.136473
2     two  C  foo  1.018601 -0.561757
3   three  A  bar -0.595447 -1.623033
4     one  B  bar  1.395433  0.029399
5     one  C  bar -0.392670 -0.542108
6     two  A  foo  0.007207  0.282696
7   three  B  foo  1.928123 -0.087302
8     one  C  foo -0.055224 -1.575170
9     one  A  bar  2.395985  1.771208
10    two  B  bar  1.552825  0.816482
11  three  C  bar  0.166599  1.100230

pivot_table()通过指定values、index和columns来透视DataFrame

In [103]: pd.pivot_table(df, values="D", index=["A", "B"], columns=["C"])
Out[103]: 
C             bar       foo
A     B                    
one   A  2.395985 -1.202872
      B  1.395433 -1.814470
      C -0.392670 -0.055224
three A -0.595447       NaN
      B       NaN  1.928123
      C  0.166599       NaN
two   A       NaN  0.007207
      B  1.552825       NaN
      C       NaN  1.018601

时间序列#

pandas 具有简单、强大且高效的功能，用于在频率转换期间执行重采样操作（例如，将秒级数据转换为 5 分钟级数据）。这在金融应用中非常常见，但不仅限于此。请参阅时间序列部分。

In [104]: rng = pd.date_range("1/1/2012", periods=100, freq="s")

In [105]: ts = pd.Series(np.random.randint(0, 500, len(rng)), index=rng)

In [106]: ts.resample("5Min").sum()
Out[106]: 
2012-01-01    24182
Freq: 5min, dtype: int64

Series.tz_localize()将时间序列本地化到某个时区

In [107]: rng = pd.date_range("3/6/2012 00:00", periods=5, freq="D")

In [108]: ts = pd.Series(np.random.randn(len(rng)), rng)

In [109]: ts
Out[109]: 
2012-03-06    1.857704
2012-03-07   -1.193545
2012-03-08    0.677510
2012-03-09   -0.153931
2012-03-10    0.520091
Freq: D, dtype: float64

In [110]: ts_utc = ts.tz_localize("UTC")

In [111]: ts_utc
Out[111]: 
2012-03-06 00:00:00+00:00    1.857704
2012-03-07 00:00:00+00:00   -1.193545
2012-03-08 00:00:00+00:00    0.677510
2012-03-09 00:00:00+00:00   -0.153931
2012-03-10 00:00:00+00:00    0.520091
Freq: D, dtype: float64

Series.tz_convert()将时区感知的时间序列转换为另一个时区

In [112]: ts_utc.tz_convert("US/Eastern")
Out[112]: 
2012-03-05 19:00:00-05:00    1.857704
2012-03-06 19:00:00-05:00   -1.193545
2012-03-07 19:00:00-05:00    0.677510
2012-03-08 19:00:00-05:00   -0.153931
2012-03-09 19:00:00-05:00    0.520091
Freq: D, dtype: float64

向时间序列添加非固定时长（BusinessDay）

In [113]: rng
Out[113]: 
DatetimeIndex(['2012-03-06', '2012-03-07', '2012-03-08', '2012-03-09',
               '2012-03-10'],
              dtype='datetime64[ns]', freq='D')

In [114]: rng + pd.offsets.BusinessDay(5)
Out[114]: 
DatetimeIndex(['2012-03-13', '2012-03-14', '2012-03-15', '2012-03-16',
               '2012-03-16'],
              dtype='datetime64[ns]', freq=None)

分类数据#

pandas 可以在DataFrame中包含分类数据。有关完整文档，请参阅分类简介和API 文档。

In [115]: df = pd.DataFrame(
   .....:     {"id": [1, 2, 3, 4, 5, 6], "raw_grade": ["a", "b", "b", "a", "a", "e"]}
   .....: )
   .....:

将原始等级转换为分类数据类型

In [116]: df["grade"] = df["raw_grade"].astype("category")

In [117]: df["grade"]
Out[117]: 
0    a
1    b
2    b
3    a
4    a
5    e
Name: grade, dtype: category
Categories (3, object): ['a', 'b', 'e']

将类别重命名为更有意义的名称

1
2
3

In [118]: new_categories = ["very good", "good", "very bad"]

In [119]: df["grade"] = df["grade"].cat.rename_categories(new_categories)

重新排序类别并同时添加缺失的类别（Series.cat()下的方法默认返回一个新的Series）

In [120]: df["grade"] = df["grade"].cat.set_categories(
   .....:     ["very bad", "bad", "medium", "good", "very good"]
   .....: )
   .....: 

In [121]: df["grade"]
Out[121]: 
0    very good
1         good
2         good
3    very good
4    very good
5     very bad
Name: grade, dtype: category
Categories (5, object): ['very bad', 'bad', 'medium', 'good', 'very good']

排序是按类别顺序，而不是字典顺序

In [122]: df.sort_values(by="grade")
Out[122]: 
   id raw_grade      grade
5   6         e   very bad
1   2         b       good
2   3         b       good
0   1         a  very good
3   4         a  very good
4   5         a  very good

使用 observed=False 按分类列分组也会显示空类别

In [123]: df.groupby("grade", observed=False).size()
Out[123]: 
grade
very bad     1
bad          0
medium       0
good         2
very good    3
dtype: int64

绘图#

请参阅绘图文档。

我们使用标准约定来引用 matplotlib API

1
2
3

In [124]: import matplotlib.pyplot as plt

In [125]: plt.close("all")

plt.close 方法用于关闭图形窗口

In [126]: ts = pd.Series(np.random.randn(1000), index=pd.date_range("1/1/2000", periods=1000))

In [127]: ts = ts.cumsum()

In [128]: ts.plot();

../_images/series_plot_basic.png

plot()绘制所有列

In [129]: df = pd.DataFrame(
   .....:     np.random.randn(1000, 4), index=ts.index, columns=["A", "B", "C", "D"]
   .....: )
   .....: 

In [130]: df = df.cumsum()

In [131]: plt.figure();

In [132]: df.plot();

In [133]: plt.legend(loc='best');

../_images/frame_plot_basic.png

导入和导出数据#

请参阅IO 工具部分。

CSV#

写入 CSV 文件：使用DataFrame.to_csv()

1
2
3

In [134]: df = pd.DataFrame(np.random.randint(0, 5, (10, 5)))

In [135]: df.to_csv("foo.csv")

从 CSV 文件读取：使用read_csv()

In [136]: pd.read_csv("foo.csv")
Out[136]: 
   Unnamed: 0  0  1  2  3  4
0           0  4  3  1  1  2
1           1  1  0  2  3  2
2           2  1  4  2  1  2
3           3  0  4  0  2  2
4           4  4  2  2  3  4
5           5  4  0  4  3  1
6           6  2  1  2  0  3
7           7  4  0  4  4  4
8           8  4  4  1  0  1
9           9  0  4  3  0  3

Parquet#

写入 Parquet 文件

1	In [137]: df.to_parquet("foo.parquet")

使用read_parquet()从 Parquet 文件读取

In [138]: pd.read_parquet("foo.parquet")
Out[138]: 
   0  1  2  3  4
0  4  3  1  1  2
1  1  0  2  3  2
2  1  4  2  1  2
3  0  4  0  2  2
4  4  2  2  3  4
5  4  0  4  3  1
6  2  1  2  0  3
7  4  0  4  4  4
8  4  4  1  0  1
9  0  4  3  0  3

Excel#

读写Excel。

使用DataFrame.to_excel()写入 Excel 文件

1	In [139]: df.to_excel("foo.xlsx", sheet_name="Sheet1")

使用read_excel()从 Excel 文件读取

In [140]: pd.read_excel("foo.xlsx", "Sheet1", index_col=None, na_values=["NA"])
Out[140]: 
   Unnamed: 0  0  1  2  3  4
0           0  4  3  1  1  2
1           1  1  0  2  3  2
2           2  1  4  2  1  2
3           3  0  4  0  2  2
4           4  4  2  2  3  4
5           5  4  0  4  3  1
6           6  2  1  2  0  3
7           7  4  0  4  4  4
8           8  4  4  1  0  1
9           9  0  4  3  0  3

常见陷阱#

如果您尝试对Series或DataFrame执行布尔操作，可能会看到类似以下的异常：

In [141]: if pd.Series([False, True, False]):
   .....:      print("I was true")
   .....: 
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-141-b27eb9c1dfc0> in ?()
----> 1 if pd.Series([False, True, False]):
      2      print("I was true")

~/work/pandas/pandas/pandas/core/generic.py in ?(self)
   1575     @final
   1576     def __nonzero__(self) -> NoReturn:
-> 1577         raise ValueError(
   1578             f"The truth value of a {type(self).__name__} is ambiguous. "
   1579             "Use a.empty, a.bool(), a.item(), a.any() or a.all()."
   1580         )

ValueError: The truth value of a Series is ambiguous. Use a.empty, a.bool(), a.item(), a.any() or a.all().

请参阅比较和常见陷阱以获取解释和解决方法。

留言與分享

23. 最小生成树

2015 年 3 月 15 日分類算法

23. 最小生成树

引：在设计电子电路时，我们常常需要将多个组件的针脚连起。若要连接n个针脚，可以用n-1根连线，我们希望使用的最短的连线来连接针脚。

最小生成树问题：
一个连通无向图 $G = (V, E)$ 中，对于每条边 $(u, v) \in E$ ，为其赋予权重 $w(u, v)$ 。找到一个无环子集 $T \subseteq E$ ，使得所有的结点可以互相到达，并且具有最小的权重，即： $w(T) = \sum_{(u, v) \in T}w(u, v)$ 的值最小。 $T$ 就是图 $G$ 的最小生成树。

下图中阴影部分组成的就是最小生成树。

生成最小生成树

本章将介绍两种生成最小生成树的算法，他们都用了贪心策略。

思想：创建一个边的集合A，首先讲集合A设置为空集，每次循环加入一条安全的边到集合A中，是的A是最小生成树T的子集，直到集合A覆盖了所有结点。

下面是这个贪心策略的伪代码：

如何找出一个安全的边

这个贪心策略的重点就是如何找出安全的边。

设边集合A覆盖的结点集合为S，没覆盖到的结点集合为V-S。想要生成最小生成树，则必须有且仅有一条边连接S和V-S（连接两个集合的意思为边的一头在S中，另一头在V-S中），所有连接S和V-S的边中权重最小的边就是安全的边。

可以用反证法证明这种选择安全的边的方法是正确的。

Kruskal算法

思想：初始时，将 $|V|$ 个结点视为 $|V|$ 棵树并组成森林。所有边的权重按照从小到大排序，从最小的边开始编译，如果这个边能连接森林中的两棵树，则将这条边加入集合A，并且将这两棵树合并为一棵树。直到森林中只剩一棵树。

伪代码和事例如下：

Prim算法

思想：初始时，给所有的结点赋予一个无穷大的key值，并加入优先队列。每次循环时，从优先队列中取出一个key值最小的结点u加入集合A中，并且更新优先队列中所有与结点u相连的结点v的key值（如果 $w(u,v) < v.key$ ，则 $v.key = w(u,v)$ ）。直到优先队列为空。

伪代码和事例如下：

TODO:时间复杂度分析

留言與分享

22. 基本的图算法

2015 年 3 月 13 日分類算法

22. 基本的图算法

本章介绍图的表示和搜索。
许多的图算法在一开始都会先通过搜索来获得图的结构，其他一些图算法则是对基本的搜索加以优化。
可以说，图的搜索技巧是整个图算法领域的核心。

图的表示

$G = (V, E)$

图G由结点的集合V 和边的集合E 组成

可以用两种方法表示，一种是邻接链表（下图b），一种是邻接矩阵（下图c）。
邻接链表一般用于表示稀疏图（边数 $|E|$ 远小于 $|V|^2$ ），默认都使用邻接链表表示。在稠密图（ $|E|$ 接近 $|V|^2$ ）的情况下，倾向使用邻接矩阵。

无向图：

有向图：

邻接链表表示

由一个链表数组 $Adj$ 组成，数组大小为 $|V|$ ，链表 $Adj[u]$ 存储了结点 $u$ 出发的边的终点。
比如上面无向图中，从结点1出发有两条边，边的终点分别是2和4，反应到邻接链表中就是 $Adj[1]$ 存储了两个节点2和4。

邻接链表需要的存储空间为 $\Theta(|V|+|E|)$

邻接矩阵表示

由一个 $|V| \times |V|$ 的矩阵 $A = (a_{ij})$ 表示，并满足以下条件：

$a_{ij} = \left \{ \begin{aligned} & 1 & if (i, j) \in E, &\\ & 0 & other, & \end{aligned} \right.$

当边有权重时， $a_{ij}$ 可以存储权重值。

邻接矩阵需要的存储空间为 $\Theta(|V|^2)$

一些术语

一个结点的出度为，从这个结点触发的边的个数。
一个结点的入度为，到达这个结点的边的个数。

广度优先搜索

思路：利用一个队列，首先将头结点插入队列，循环的取出队列中的一个结点，并将于该结点相连的结点加入队列，直到队列变空，搜索结束。

辅助的给每个结点加入三个属性：

color：白色表示还未被搜索，灰色表示加入队列，黑色表示从队列里出来
d：该节点在第几轮被发现
$\boldsymbol{\pi}$ ：该结点的前驱（结点第一次被发现时，正在查询的结点）

下面是广度优先搜索的伪代码和事例：

广度优先搜索的正确性

TODO

广度优先搜索的性质

最短路径

从某个结点u做广度优先搜索，可以找出这个结点到其他结点的最短路径。

结点v和结点u的最短路径距离为v.d

从结点v开始循环列举前驱结点，就是结点v和结点u的最短路径中经过的结点。

广度优先树

广度优先搜算中，我们在 $\pi$ 属性中存储了每个结点的前驱结点，另前驱结点作为该结点的父节点，我们可以得到一个广度优先树。发现新结点的边为树边。

深度优先搜索

思路：尽可能的深入。总是对最近发现的结点v出发的边进行探索，直到结点v出发的边全部被发现时，回溯到v的前驱结点继续探索，直到从源节点出发所有可以到达的结点都被发现。这时如果还有未被搜索的结点，则再随机找一个未被搜索的结点作为源节点进行搜索。

因为可能从一个源节点出发不能搜索到所有结点，所以深度优先搜索会产生多个深度优先树组成深度优先深林。

辅助的给每个结点加入四个属性：

color：白色表示还未被搜索，灰色表示已被发现但出发的边还没搜索完，黑色表示已被发现并且出发的边已被搜索完
d：该节点的发现时间
f：该结点出发搜索结束的时间
$\boldsymbol{\pi}$ ：该结点的前驱（结点第一次被发现时，正在查询的结点）

下面是深度优先搜索的伪代码和事例：

结点中的x/y表示该结点的发现时间为x，完成时间为y
图中树边被标记为灰色，向前，横向，向前的边分别被标记为B, C, F

深度优先搜索的性质

括号花定理

如上图b所示，每个结点的发现时间和完成时间组成一个括号花结构。

对于两个结点u和v，如果区间[u.d, u.f] 和 [v.d, v.f] 不相交，则u不是v的后代，v也不是u的后代；
如果[u.d, u.f] 包含在 [v.d, v.f] 内，则u是v后代，反之亦然。

白色路径定理

如果结点v是u的后代，当u.d时间时，存在一条从u到v全部由白色结点组成的路径。

拓扑排序

对于有向无环图 $G = (V, E)$ ，其拓扑排序是G种所有结点的一种线性次序，该次序满足如下条件：如果G包含边(u, v)，则结点u在拓扑排序中处于结点v的前面。

许多实际应用都需要使用有向无环图来说明事件的优先次序。

下图是一个穿衣服的实例，图a中表示了穿戴某一件衣物的依赖关系，图b是图a拓扑排序的结果，按照图b相反的顺序穿衣服就是没问题的了。

拓扑排序的思想为：对图G做DFS，然后按照结点搜索的完成时间逆序排序。伪代码如下：

拓扑排序的正确性：在向无环图中，如果有变(u, v)，那么v肯定比u先完成搜索。

强联通分量

有向图 $G = (V, E)$ 的强连通分量是一个最大结点集合 $C \subseteq V$ ，对于该集合的任意一对结点可以互相到达。

下图a的灰色覆盖区域就是图的强联通分量。

算法伪代码如下：

对G做DFS，并记下每个结点的完成时间u.f
转置G，得到 $G^T$ ，如上图b
按照u.f大小，从大到小对 $G^T$ 做DFS
第三步得到的深度优先深林中，每棵深度优先树的结点都组成为G的一个强联通分量

思想：
对于分量图 $G^{SCC} = (V^{SCC}, E^{SCC})$ ， $V^{SCC} = {v_1, v_2, ... , v_k}$ ，图 $G$ 中的强联通分量 $C_i$ 集合代表分量图中的结点 $v_i$ ：如果有 $x\in C_i, y\in C_j$ ，且图 $G$ 中有边 $(x, y)$ ，则边 $(v_i, v_j) \in E^{SCC}$ ，且图 $G^{SCC}$ 是有向无环图。

证明：
引理1： $C$ 和 $C^\prime$ 是图 $G$ 的两个强连通分量。当 $u, v \in C; u^\prime, v^\prime \in C^\prime$ ，若有 $u \rightsquigarrow u^\prime$ ，则不可能有 $v^\prime \rightsquigarrow v$ 。
可用反证法证明，若有 $u \rightsquigarrow u^\prime$ 且 $v^\prime \rightsquigarrow v$ ，则 $C$ 和 $C^\prime$ 将成为同一个强连通分量。
引理2： $C$ 和 $C^\prime$ 是图 $G$ 的两个强连通分量。当 $(u, v) \in E$ 且 $u \in C, v \in C^\prime$ ，则 $f(C) > f(C^\prime)$
当 $d(C) < d(C^\prime)$ 时，若 $x$ 为 $C$ 中最早被发现的结点，则 $C$ 和 $C^\prime$ 中的其它结点都是 $x$ 的子孙，也就是所有结点的完成时间都比 $x$ 早，所以 $x.f=f(C)>f(C^\prime)$
当 $d(C) > d(C^\prime)$ 时，根据引理1，没有从 $C$ 到 $C^\prime$ 的边，也就是 $C^\prime$ 完成之后不会到达任意 $C$ 中的结点，所以 $f(C)>f(C^\prime)$
引理3： $C$ 和 $C^\prime$ 是图 $G$ 的两个强连通分量。当 $(u, v) \in E^T$ 且 $u \in C, v \in C^\prime$ ，则 $f(C) < f(C^\prime)$
$(u, v) \in E^T \Longrightarrow (v, u) \in E$ ，由引理2可直接得知 $f(C) < f(C^\prime)$
证明：根据数学归纳法，假设算法第三行所生成的前 $k$ 棵树都是强连通分量，现在需要考虑第 $k+1$ 棵树是否为强连通分量：
设第 $k+1$ 棵树是 $C$ ， $C$ 的根节点为 $u$ ， $u$ 所在的强连通分量为 $C^{\prime\prime}$ 。
若 $G^T$ 中从 $C^{\prime\prime}$ 到其他强连通分量 $C^{\prime\prime\prime}$ 有边，那么根据引理3可知 $f(C^{\prime\prime}) < f(C^{\prime\prime\prime})$ 。
而算法对 $G^T$ 做DFS时，是按照 $f$ 大小逆序进行，所以从 $C^{\prime\prime}$ 出来的变都是到前 $k$ 棵树的。
所以 $C=C^{\prime\prime}$ ，也就是说第 $k+1$ 棵树为强连通分量。

留言與分享

17. 摊还分析

2015 年 3 月 12 日分類算法

17. 摊还分析

在摊还分析中，我们求数据结构的一个操作序列中所执行的所有操作的平均时间，来评价操作的代价。这样，我们就可以说明一个操作的平均代价是很低的，即使序列中某个单一操作的代价很高。摊还分析不同于平均情况分析，它并不涉及概率，它可以保证最坏情况下每个操作的平均性能。

本章介绍三种摊还分析方法：

聚合分析
核算法
势能法

首先我们先看两个小问题

栈操作

对传统的栈操作MULTIPOP(S, k)扩展，伪代码如下，相当于做k次POP(S)

MULTIPOP(S, k)
1   while not STACK-EMPTY(S) and k > 0
2       POP(S)
3       k = k - 1

如果在一个包含s个对象的栈上做MULTIPOP(S, k)操作，POP的次数为min(s, k)。

我们来分析一个由n个PUSH/POP/MULTIPOP组成的操作序列在一个空栈上的执行情况。
MULTIPOP的最坏代价为 $O(n)$ ，那么n个操作的最坏代价是 $O(n^2)$ 吗？

二进制计数器递增

k位二进制计数器递增，初始值为0。用一个位数组A[0…k-1]作为计数器。当计数器保存二级制数x时，x的最低位保存在A[0]中，最高位保存在A[k-1]中，因此 $x = \sum\limits_{i=0}^{k-1}A[i]\cdot 2^i$ 。INCREMENT的伪代码如下：

INCREMENT(A)
1   i = 0
2   while i < A.length and A[i] == 1
3       A[i] = 0
4       i = i + 1
5   if i < A.length
6       A[i] = 1

可以想象，最坏情况当k位全部是1时，INCREMENT操作要做k次翻转操作，也就是要花费 $\Theta(k)$ 时间，所以对初值为0的计数器，做n次操作的最坏情况花费 $O(nk)$ 次操作？

从上两个问题，我们都根据一个操作最坏情况的时间消耗推测，整个操作序列的时间消耗，显然不是一个确界。下面我们通过三种摊还分析方法来分析这两个问题中每个操作的平均代价（摊还代价）。

聚合分析

聚合分析——确定n个操作最坏情况的总代价 $T(n)$ ，所以每个操作的平均代价为 $T(n)/n$ 。

栈操作：
虽然单独的MULTIPOP操作可能代价很高，但在一个空栈上实行n个操作，POP和MULTIPOP操作的总消耗最多为O(n)，因为只有push进去数据，POP和MULTIPOP才会有消耗，而且PUSH操作每次只能push一个数据进来。所以n个操作最坏情况的总代价为O(n)，除以n得到每个操作的平均代价为O(1)。

二进制计数器递增：
下图展示了二进制计数器从0递增到16的过程，阴影部分表示递增后需要翻转的位。我们可以发现A[0]每次递增时都发生翻转，A[1]每两次递增发生一次翻转，A[2]每四次递增发生一次翻转，以此类推第i位每 $2^i$ 次递增发生一次翻转。也就是说n次INCREMENT操作后，第i位会翻转 $\lfloor n/2^i\rfloor$ 次。
执行n次INCREMENT操作产生的总翻转次数为：

$\sum_{i=0}^{k-1}\lfloor n/2^i\rfloor < n\sum_{i=0}^\infty \frac{1}{2^i} = 2n$

所以，n个INCREMENT操作的最坏情况用时为O(n)，除以n得到每个操作的平均代价为O(1)。

核算法

核算法——对不同的操作赋予不同的费用（可以大于或者小于实际的代价，但不能为负值），称其为摊还代价。当一个操作摊还代价大于实际代价时，我们将差额存起来，称其为信用/存款。后续操作如果有摊还代价小于实际代价时，我们将之前存的信用拿出一部分来抵消这里的差值。如果用 $c_i$ 表示第i个操作的实际代价，用 $\hat{c}_i$ 表示第i个操作的摊还代价，则对任意n个操作的序列，要求：

$\sum_{i=1}^n \hat{c}_i \ge \sum_{i=1}^n c_i$

信用总能刚好抵债或者有剩余，从而使得总的摊还代价为总实际代价的上界。

栈操作：
栈操作的实际代价如下：

1
2
3

PUSH       1
POP        1
MULTIPOP   min(k, s)

我们将栈操作的摊还代价设置为：

1
2
3

PUSH       2
POP        0
MULTIPOP   0

每次PUSH操作支付1的实际代价，剩下的1存起来。存起来的钱和堆栈里的数据量相同，而POP或MULTIPOP操作的实际代价为要pop的数据量，所以存款总能保证大于等于零。
每个操作的摊还代价都是常数，所以总的摊还代价为O(n)。

二进制计数器递增：
将INCREMENT中的操作分为置位操作（第6行，0->1）和复位操作（while循环中的操作，1->0）。令置位操作的摊还代价为2，复位操作的摊还代价为0。每次置位操作可以多出1存起来（存起来的钱和计数器中1的个数相同），复位操作需要预支存款，但复位操作只有当某一位是1的时候才会执行，由于计数器中1的个数永远不会为负，所以存款总能保证大于等于零。
每个操作的摊还代价都是常数，所以总的摊还代价为O(n)。

势能法

势能法将数据结构和势能关联起来——对一个初始化数据结构 $D_0$ 执行n个操作。 $c_i$ 为第i个操作的实际代价， $D_i$ 为第i次操作后的数据结构。势函数 $\Phi$ 将每个数据结构 $D_i$ 映射到一个实数 $\Phi(D_i)$ ，为数据结构 $D_i$ 的势。第i个操作的摊还代价 $\hat{c}_i$ 用势函数 $D_0$ 定义为：

\textrm{公式1：} \hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1})

即，每个操作的摊还代价为实际代价加上操作引起的势变化。所以总摊还代价为：

\textrm{公式2：}\sum_{i=1}^n \hat{c}_i = \sum_{i=1}^n (c_i + \Phi(D_i) - \Phi(D_{i-1})) = \sum_{i=1}^n c_i + \Phi(D_n) - \Phi(D_{0})

根据公式1可以得到每个步骤的摊还代价，从而算出总的摊还代价，然后根据公式2可以得出总实际代价的上界/下界（ $\Phi(D_n) - \Phi(D_{0})$ 为正数则得到上界， $\Phi(D_n) - \Phi(D_{0})$ 为负数则得到下界）。

``````````````	核算法	势能法
摊还代价	猜想/推测得到	通过实际代价加势能变化得到
思想	较为简单	较为抽象
难点	需要证明存款足以抵债	需要考虑一个好的势函数
优势	考虑起来较为容易	应用范围广，适用的场景更多
联系	核算法的存款往往能和势能法的势函数相对应	势能法中计算摊还代价时，当势差为正数时相当于将势差作为存款存起来，当势差为负数时相当于要用存款中拿出部分来抵债，所以两种方法的内涵是一致的

栈操作：
将势函数定义为当前栈中的数据量。
PUSH操作会压入一个数据，所以势差为1，而且实际代价为1，所以PUSH操作的摊还代价为2。
POP/MULTIPOP操作会弹出x个对象，所以势差为-x，而实际代价为x，所以POP/MULTIPOP操作的摊还代价为0。

栈每个操作的摊还代价都是O(1)，所以n个操作的总摊还代价为O(n)。由于初始的栈为空，而结束时栈的数据量大于等于0，也就是说 $\Phi(D_n) - \Phi(D_{0})$ 为正数，所以n个操作的总摊还代价为总实际代价的上界O(n)。

二进制计数器递增：
将势函数定义为计数器中1的个数 $b_i$ 。
假设第i个操作将 $t_i$ 个位复位，则实际代价为 $t_i + 1$ ，因为还有一次置位操作。
再来考虑摊还代价，如果 $b_i$ 为0，则将k位都复位了，因此 $b_{i-1} = t_i = k$ 。
如果 $b_i>0$ ，则 $b_i = b_{i-1} - t_i + 1$ 。无论那种情况都有 $b_i \le b_{i-1} - t_i + 1$ ，所以摊还代价为：

$\hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1}) \le (t_i + 1) + (-t_i + 1) = 2$

所以总摊还代价的上界为O(n)，由于计数器初始状态为0，而1的个数不会为负数，所以n个操作的总摊还代价为总实际代价的上界O(n)。

势能法的还有个优势就是，我们可以简单的得出当初始状态不是0时实际代价的上界。由公式2可得：

$\sum_{i=1}^n c_i \le \sum_{i=1}^n 2 - b_n + b_0 = 2n -b_n + b_0 \le 2n + b_0 \le 2n + k$

所以只要 $k=O(n)$ 那么总实际代价就是O(n)。

动态表

11章介绍了散列表，我们知道散列表的大小和数据量应该是线性相关的，数据太稀疏会浪费空间，数据太稠密会浪费时间。当我们不知道会有多少数据插入时，就没办法确定散列表的大小，所以要引进动态表。
表扩张——当插入数据时发现散列表的装载因子为1（表的大小和数据量相同），对表进行扩张，比如扩张为两倍大小，首先创建一个两倍大小的表，将原来散列表中的数据插入新创建的表中，然后插入新的数据，最后不能忘了把老的表析构。

表收缩——当删除数据时发现散列包的装载因子小于某个值，对表进行收缩，与表的扩张类似，比如收缩为原来表大小的一半，首先删除这个数据并创建一般大小的新表，将原来散列表中的数据插入新创建的表中，然后把老的表析构。

表收缩时判断的装载因子的选择很重要，如果表扩张选择的两倍大小，而表收缩是选择装载因子为二分之一，这时如果在表扩张后立马删除数据，又反复的插入，删除数据，这样会导致表大小的震荡。这种情况下时间机器浪费时间。
所以我们通常可以选择该装载因子为四分之一来避免这个问题。

无论是表扩张还是表收缩，我们都可以用平摊分析来证明动态表的插入和删除操作的平均代价还是O(1)。详细情况参考书中内容，这里不做赘述。

留言與分享

16. 贪心算法

2015 年 3 月 11 日分類算法

16. 贪心算法

求解最优化问题的算法通常需要经过一系列的步骤，在每个步骤都面临多种选择。对于许多最优化问题，使用动态规划算法来求最优解有些杀鸡用牛刀了，可以使用更简单、更高效的算法．贪心算法就是这样的算法，它在每一步都做出当时看起来最佳的选择。也就是说，它总是做出局部最优的选择，寄希望这样的选择能导致全局最优解。

活动选择问题

我们的第一个例子是一个调度竞争共享资源的多个活动的问题，目标是选出一个最大的互相兼容的活动集合。假定有一个 n 个活动的集合 $S={a_1, a_2, ... , a_n}$ ，这些活动使用同一个资源（例如一个阶梯教室），而这个资源在某个时刻只能供一个活动使用。每个活动 $a_i$ 都有一个开始时间 $s_i$ 和一个结束时间 $f_i$ ，其中 $0\le s_i < f_i < \infty$ 。如果被选中，任务 $a_i$ 发生在半开时间区间 $[s_i, f_i)$ 期间．如果两个活动 $a_i$ 和 $a_j$ 满足 $[s_i, f_i)$ 和 $[s_j, f_j)$ 不重叠，则称它们是兼容的．也就是说，若 $s_i\ge f_j$ 或 $s_j\ge f_i$ ，则 $a_i$ 和 $a_j$ 是兼容的．在活动选择问题中，我们希望选出一个最大兼容活动集。假定活动已按结束时间的单调递增顺序排序：

$f_1 \le f_2 \le f_3 \le ... \le f_{n-1} \le f_n$

例如下面的活动集合S：

i	1	2	3	4	5	6	7	8	9	10	11
$s_i$	1	3	0	5	3	5	6	8	8	2	12
$f_i$	4	5	6	7	9	9	10	11	12	14	16

对于这个例子，子集 $S={a_3, a_9,a_11}$ 由相互兼容的活动组成。但它不是一个最大集，因为子集 $S={a_1, a_4, a_8,a_11}$ 更大。实际上 $S={a_1, a_4, a_8,a_11}$ 是一个最大兼容活动子集，另一个最大子集是
$S={a_2, a_4, a_9,a_11}$ 。

最优子结构

假定集合 $S_{ij}$ （ $a_i$ 结束之后， $a_j$ 开始之前的活动）的一个最大相互兼容的活动子集为 $A_{ij}$ ，而且 $A_{ij}$ 包含了活动 $a_k$ 。由于最优解包含了活动 $a_k$ ，我们得到两个子问题： $S_{ik}$ （ $a_k$ 开始之前的活动）的兼容活动和 $S_{kj}$ （ $a_k$ 结束之后的活动）的兼容活动。由剪切-粘贴法可以证明 $S_{ij}$ 的最优解为 $S_{ik}$ 的最优解、 $a_k$ 、 $S_{kj}$ 的最优解组成。即 $A_{ij} = A_{ik} \cup a_k \cup A_{kj}$ 。
所以这时我们可以用动态规划方法求出所有k的取值情况对应的解，然后找出一个最大的作为最优解。
如果用 $c[i, j]$ 表示 $S_{ij}$ 的最优解的大小，递归式为：

$c[i, j] = \left \{ \begin{aligned} & 0 & if \quad S_{ij} = \varnothing, \\ & \max_{a_k \in S_{ij}}\{c[i, k] + c[k, j] + 1\} & if \quad S_{ij} \ne \varnothing, \end{aligned} \right.$

贪心选择

动态规划需要考虑每种子问题，比较之后得出哪种选择是最优解。假如我们无需求解每种子问题，直接就可以找出一个最优选择。那么将大大减少计算过程。对于活动选择问题，我们可以只考虑一个选择：贪心选择。

直观上，我们应该选择一个活动，使得选择它后剩下的资源可以尽可能多的被其他活动利用。直觉告诉我们选择S中最早结束的活动，因为他可以剩下尽可能多的资源。由于我们活动时按照结束时间排序的，也就是说贪心选择就是 $a_1$ 。

当做出贪心选择后，只剩下一个子问题需要求解，因为不会有在 $a_1$ 开始前结束的活动。加上前面的最优子结构性质，所以S的最优解就是 $a_1 \bigcup A_{1n}$ 。

证明贪心选择——最早结束的活动总是最优解的一部分：

定理：考虑任意非空子问题 $S_k$ ，另 $a_m$ 是 $S_k$ 种最早结束的活动，则 $a_m$ 在 $S_k$ 的某个最大兼容活动子集中。

证明： $A_k$ 是 $S_k$ 的某个最大兼容活动子集， $a_j$ 是 $A_k$ 种最早结束的活动。如果 $a_j = a_m$ ，则已经证明 $a_m$ 在 $S_k$ 的某个最大兼容活动子集中；如果 $a_j \ne a_m$ ，那么用 $a_m$ 替换 $A_k$ 中的 $a_j$ 产生 $A_k^\prime$ ，由于 $f_m \le f_j$ 而且 $A_k$ 中的活动都是不相交的，所以 $A_k^\prime$ 也是 $S_k$ 的最大兼容活动子集，得证。

递归贪心算法

为了方便算法初始化，添加一个虚拟活动 $a_0$ ，其结束时间 $f_0 = 0$ ，这样子问题 $S_0$ 就是完整的活动集S。求解原问题即可调用 RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n)。

2,3行是为了找到第一个，与 $a_k$ 不相交的最先结束的活动 $a_m$ 。

迭代贪心算法

贪心算法原理

前面我们讨论活动选择问题的贪心算法的过程比通常的过程繁琐一些，我们当时经过了如下几个步骤：

确定问题的最优子结构．
设计一个递归算法（动态规划）。
证明如果我们做出一个贪心选择，则只剩下一个子问题。
证明贪心选择总是安全的（步骤 3 、 4 的顺序可以调换）。
设计一个递归算法实现贪心策略。
将递归算法转换为迭代算法。

这个过程详细的看到贪心算法是如何以动态规划为基础的。
更一般地，我们可以简单按如下步骤设计贪心算法：

将最优化问题转化为这样的形式：对其做出一次选择后，只剩下一个子问题需要求解。
证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的。
证明做出贪心选择后，剩余的子问题满足性质：其最优解与贪心选择组合即可得到原问题的最优解，这样就得到了最优子结构。

在本章剩余部分中，我们将使用这种更直接的设计方法．但我们应该知道，在每个贪心算法之下，几乎总有一个更繁琐的动态规划算法。

在证明一个问题可以用贪心算法解决过程中，证明一个问题的贪心选择性质 和 最优子结构性质 是非常重要的。

赫夫曼编码

赫夫曼编码k而已有效的压缩数据：通常可以节省20%~90%的空间，具体压缩率依赖于数据的特型。我们将待压缩数据看做字符序列。根据每个字符出现的频率，赫夫曼贪心算法构造出字符的最优二进制表示。

下面给出一个例子，待压缩文件有10万个字符数据。文件中出现了6种不同的字符，出现的次数见表格：

	a	b	c	d	e	f
频率（千次）	45	13	12	16	9	5
定长编码	000	001	010	011	100	101
变长编码	0	101	100	111	1101	1100

如果用定长编码来存储信息，那么需要用3位来表示z和6个字符。这种方法总共需要300000个二进制位来存储。
但如果用变长编码来存储信息，如表格中所示，出现频率较高字符的使用短一点的二进制编码表示。这种方法需要 $(45 \times 1 + 13 \times 3 + 12 \times 3 + 16 \times 3 + 9 \times 4 + 5 \times 4) \times 1000 = 224000$ 位。与定长编码相比节约了25%的空间。

我们这里只考虑前缀码，即没有任何码字是其他码字的前缀。只考虑前缀码的原因是，前缀码与任何其他编码方式比都可以保证最优的压缩率，但此处不予证明。
前缀码的作用是简化解码过程，由于没有任何码字是其他码字的前缀，所以文件开头的码字是无歧义的。我们可以简单的识别出开始码字，将其转换为对应的字符，然后对文件剩余部分重复的做这种解码过程。
编码方案可以用一个二叉树表示——编码树。下图a表示了定长编码的编码树，图b表示了变长编码的编码树。叶子结点为字符，并存储字符的出现频率，字符的二进制编码是从根节点到叶子节点的路径，向左表示0，向右表示1。内部结点不存储字符，存储子节点的频率和。

给定一棵对应前缀码的树T，我们可以容易地计算出编码一个文件需要多少个二进制位。对于字母表C中的每个字符c，令属性c.freq表示c在文件中出现的频率，令 $d_T(c)$ 表示c的叶结点在树中的深度。注意， $d_T(c)$ 也是字符c的码字的长度。则编码文件需要习：

$B(T) = \sum_{c \in C}c.freq\cdot d_T(c)$

个二进制位，我们将B(T)定义为T的代价。

构造赫夫曼编码

赫夫曼设计了一个贪心算法得到最优前缀码，被称为赫夫曼编码。

下面是哈夫曼算法的伪代码，输入一个字母表C，输出一个最优前缀码对应的编码树。

构造编码树的过程如下：
算法中使用一个优先队列Q，初始化时将字母表C全部插入Q。每次循环时，创造一个结点z，从优先队列取出两个最小值作为结点z的孩子，并使得z.freq为两个孩子的freq之和，然后将z结点重新插入优先队列Q中。直到优先队列中只剩下一个元素，这时这个元素为编码树的root结点，并且所有字符都已加入编码树。

下面是一个例子：

证明赫夫曼算法的正确性

贪心选择

贪心选择性质：若x,y是C中频率最低的两个字符。那么C存在一个最优前缀码，x,y的码字长度相等，且只有最后一个二进制位不同。

证明思路，假设有一个最优前缀码的编码树 $T$ ，把x,y与编码树中深度最深的两个兄弟节点进行交换产生 $T^\prime$ 。通过计算得出 $B(T^\prime) \le B(T)$ 。

最优子结构

最优子结构性质：若x,y是C中频率最低的两个字符。令 $C^\prime$ 为 $C$ 去除x和y，然后加入字符z，且 $z.freq = x.freq + y.freq$ 。 $T^\prime$ 为 $C^\prime$ 的一个最优前缀码的编码树，将 $T^\prime$ 中的叶子节点z替换为一个以x,y为子节点的内部节点得到树 $T$ 。则T为C的一个最优前缀码的编码树。

证明思路，反证法，假设C存在一个 $T^{\prime\prime}$ 比T更优，由贪心选择性质可知x,y为兄弟节点（不一定吧？书中用不失一般性，不太理解），将 $T^{\prime\prime}$ 中的x,y替换为z得到 $T^{\prime\prime\prime}$ ，结果得到 $B(T^{\prime\prime\prime}) < B(T^{\prime})$ ，与 $T^\prime$ 为 $C^\prime$ 的一个最优前缀码的编码树的假设相悖。

涉及算法

点击查看实现

活动选择问题
赫夫曼编码

留言與分享

15. 动态规划

2015 年 3 月 10 日分類算法

15. 动态规划

动态规划和分治法相似，都是通过组合子问题的解来求解原问题的解。但不同的是分治法将问题划分为不相交的子问题，递归的求解子问题，再将它们的解组合起来，求出原问题的解。相反，动态规划应用于子问题相互重叠的情况，即不同的子问题具有公共的子子问题。这种情况下，用分治法会反复的求解相同的子问题，造成时间浪费。动态规划对每个子问题只求解一次，并且保存在表格中，从而避免重复计算。

动态规划通常用于求解最优化问题。

我们通常按照如下步骤设计一个动态规划算法：

刻画一个最优解的结构特点
递归的定义最优解的值
计算最优解的值，通常采用自底而上的方法
利用计算出的信息构造一个最优解

如果只需要最优解的值，而非最优解本身，可忽略第四步。如果需要做第四步，往往需要在执行第三步时维护一些额外信息。

钢条切割

钢条切割问题：给定一段长度为n英寸的钢条和一个价格表p_i(i=1,2…n)，求切割方案使得收益r_n最大。

钢条切割

考虑当n=4时，所有的切割方案如下，我们发现当把4英寸的钢条切割为两段2英寸长的钢条时产生的收益最大。

钢条切割

当区分1+3切法和3+1切法时，n英寸的钢条有2^n-1种切割方案。
我们可以手动得到r_i，及对应切割方案：

钢条切割

对于r_n，我们可以用更短的钢条的最优切割收益来描述它：
$r_n = max(p_n, r_1+r_{n-1}, r_2+r_{n-2},...,r_{n-1}+r_1) .$

这时我们找到了钢条切割问题的最优子结构。每次切割后我们可以把切开的两段钢条看做独立的钢条切歌问题。一段钢条的最优解为所有切割方案中最大的。
我们可以将r_n的式子简化为： $r_n=\max\limits_{1\le i\le n}(p_i+i_{n-i})$ .

自顶而下的递归实现

根据上面的式子，我们可以得到下面这种自顶而下的递归实现（p为价格数组）：
钢条切割

这种实现的递归式为： $T(n) = 1 + \sum\limits_{j=0}^{n-1}T(j).$
我们可以求得 $T(n) = 2^i$ ，这个时间是非常惊人的，而这么大的原因就是因为包含了非常多的重复计算。下图是递归树，红线圈起来的都是重复计算部分。

钢条切割

使用动态规划方法

带备忘的自顶而下法
与前面的递归方法类似，但是用了一个数组r[1…n]记录最优解，如果发现r[n]已经有记录，则无需重复计算，直接返回该值。
自底而上法
自底而上法采用子问题的自然顺序，依次求解规模为j=1,2…,n的子问题。

无论是带备忘的自顶而下法还是自底而上法，其中都是用了一个额外数组来存储子问题的最优解，从而避免重复计算子问题的解。动态规划付出额外的内存空间来节省时间，是典型的时空权衡的例子。

子问题图

当思考动态规划问题时，弄清所涉及子问题及子问题之间的依赖关系很关键。
问题的子问题图准确的表达了这些信息：

途中结点表示钢条切割的子问题规模，箭头表示子问题之间的依赖关系。
有了子问题图，我们便可轻易的得知自底而上的顺序应该如何。
而且子问题图G=(V, E)还可以帮助我们确定动态规划算法的运行时间。由于每个子问题只求解一次，因此算法运行时间等于每个子问题求解时间之和。通常，一个子问题的求解时间与子问题图中对应顶点的度（射出边的数目）成正比，而子问题的数目等于子问题图的顶点数。因此，通常情况下，动态规划算法的运行时间与顶点和边数量呈线性关系。

重构解

前面的方法只给出的如何求出最优解的值，但并未返回解本身。
下面是基于自底而上动态规划算法的扩展，其中用数组s[0…n]存储n英寸钢条的最优切割方案，s[i]存储的数字表示，i英寸的钢条切割为s[i]英寸和i-s[i]英寸时最优，其中s[i]英寸部分不再切割，i-s[i]英寸部分的最优解需要递归查看。
所以可以通过PRINT-CUT-ROD-SOLUTION来打印出n英寸钢条的一个最优切割方案。

矩阵链乘法

给定一个n个矩阵的序列（矩阵链） $<A_1, A_2, ..., A_n>$ ，我们希望求他们的乘积 $A_1A_2...A_n$ ，由矩阵乘法的结合律我们可知给乘积链随意的加上括号不会改变最终的结果，但是不同的括号会影响矩阵链乘法的时间。
以矩阵链 $<A_1, A_2, A_3>$ 为例，三个矩阵的规模分别是10×100、100×5和5×50。如果按照 $((A_1A_2)A_3)$ 的顺序计算， $A_1A_2$ （规模10×5）需要做10×100×5=5000次标量乘法，再与 $A_3$ 相乘又需要10×5×50=2500次标量乘法，总共需要7500次标量乘法。如果按照 $(A_1(A_2A_3))$ 的顺序计算， $A_2A_3$ （规模100×50）需要做100×5×50=25000次标量乘法，A₁再与之相乘又需要10×100×50=50000次标量乘法，总共需要75000次标量乘法。因此，按照 $((A_1A_2)A_3)$ 的顺序比按照 $(A_1(A_2A_3))$ 的顺序快了10倍。
所以引入了矩阵链乘法问题：给定n个矩阵的链 $<A_1, A_2, ..., A_n>$ ，矩阵i的规模为 $p_{i-1} \times p_i$ ，求一个完全括号化方案，使得计算乘积 $A_1A_2...A_n$ 所需的标量乘法次数最少。

我们可以用下面这个递归式表示矩阵链完全括号化方案的个数，这个递归式的解为 $\Theta(2^n)$ ，所以穷举法是不可行的。

$P(n) = \left \{ \begin{aligned} & 1 & if \quad n = 1, \\ & \sum_{k=1}^{n-1}P(k)P(n-k) & if \quad n \ge 2, \end{aligned} \right.$

动态规划法

刻画一个最优解的结构特点
用 $A_{i..j}$ 表示 $A_iA_{i+1}...A_j$ 。我们可以将 $A_{i..j}$ 分解为子问题 $A_{i..k}$ 和 $A_{k+1..j}$ ，即 $A_iA_{i+1}...A_j -> (A_iA_{i+1}...A_k)(A_{k+1}A_{k+2}...A_j)$ 。然后在对子问题递归求解。
递归的定义最优解的值
用 $m[i,j]$ 表示 $A_{i..j}$ 所需标量乘法次数的最优值。假设 $A_{i..j}$ 的最优分割点为 $k(i<=k<j)$ ，那么 $m[i,j] = m[i,k] + m[k+1,j] + p_{i-1} p_{k} p_{j}$ ，然而这个分割点我们是不知道的，但是肯定在i和j之间，我们只需找到所有可能中的最小值，所以我们有如下递归式：

$m[i,j] = \left\{ \begin{aligned} & 0 & if \quad i = j, \\ & \min_{i\le k\le j}\{m[i,k] + m[k+1, j] + p_{i-1}p_kp_j\} & if \quad i < j, \end{aligned} \right.$

计算最优解的值，通常采用自底而上的方法
从上面的递归式能推测出自底而上法的顺序，或者使用子问题图辅助。可以从链长为2的子问题开始求解，一直递增到链长为n的子问题，Done。伪代码如下：

使用m[i,j]存储A_i…j的最优解的值，s[i,j]存储A_i…j的最优分割点k。
利用计算出的信息构造一个最优解
利用s数组存储的最优分割点，我们可以递归的构造出一个最优解，伪代码如下：

动态规划原理

虽然已经介绍了两个动态规划问题，但可能还会疑惑到底什么样的问题可以使用动态规划方法解决？
适合用动态规划的最优化问题应该具备两个要素：最优子结构和子问题重叠

最优子结构

动态规划法的第一步便是刻画最优解的结构。如果一个问题的最优解包括子问题的最优解，我们称此问题具有最优子结构性质。
发掘最优子结构性质的过程遵循如下通用模式：

证明问题最优解的第一个组成部分是做出一个选择
对于一个给定问题，假定已经知道哪种选择会得到最优解
给定可获得最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好的刻画子问题空间
利用“剪切-粘贴”技术证明：作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。

利用反证法：假设子问题的解不是其最优解，那么我们可以“剪切”掉这个非最优解，将最优解“粘贴”进去，从而得到一个更优的解，这与最初的解是原问题最优解的前提假设矛盾。

对于不同问题领域，最优子结构的不同体现在：

原问题的最优解涉及多少个子问题（一个问题分解为多少个子问题）
在确定最优解使用那些子问题时，我们需要考虑多少种选择（有多少种分解方式）

重叠子问题

如果递归算法反复求解相同的子问题，我们就称最优化问题具有重叠子问题性质。与之相对的，适合用分治法求解的问题通常在递归的每一步都生成全新的子问题。
动态规划通常这样利用重叠子问题的性质：对每个子问题只求解一次，将解存入一个表中，当再次需要这个子问题时直接查表，查表的代价为常数时间。

最长公共子序列

一个给定序列的子序列是降给定序列中零个或者多个元素去掉后的结果。
给定两个序列X和Y，如果Z既是X的子序列，又是Y的子序列，那么Z为X和Y的公共子序列。
最长公共子序列问题给定两个序列X={x₁, x₂, …, x_m}和Y={y₁, y₂, …, y_n}，求X和Y长度最长的公共子序列。

刻画一个最优解的结构特点
递归的定义最优解的值

$c[i,j] = \left\{ \begin{aligned} & 0 & & if \quad i = 0 \quad or \quad j = 0, \\ & c[i-1,j-1]+1 & & if \quad i,j > 0 \quad and \quad x_i = y_j, \\ & max(c[i,j-1], c[i-1, j]) & & if \quad i,j > 0 \quad and \quad x_i \neq y_j, \end{aligned} \right.$

计算最优解的值，通常采用自底而上的方法

c[i, j] 存储序列X_1->i和Y_1->j最长公共子序列的长度
b[i, j] 存储序列X_1->i和Y_1->j最优解依赖的子问题的方向
利用计算出的信息构造一个最优解

当b[i, j]存储的是“↖”时，表示x_i和y_j相同。
所以从b[m, i]开始，训着箭头方向查找“↖”，便可以找到一个最长公共子序列。
伪代码如下：

涉及算法

点击查看实现

留言與分享

14. 数据结构的扩张

2015 年 3 月 8 日分類算法

14. 数据结构的扩张

一些工程应用需要的只是教科书中的标准数据结构，也有许多其他的应用需要对现有数据结构进行少许的创新和改造，但只有很少的情况需要创造全新类型的数据结构。
更经常的是，通过存储额外信息的方法来扩张标准的数据结构，然后对这种数据结构编写新的操作来支持所需要的应用。

比如：

动态顺序统计量

之前我们讨论了中位数和顺序统计量，对于一个无序的集合，我们可以在 $\Omicron(n)$ 的时间内确认任何顺序统计量。这里我们将介绍如何修改红黑树，使得可以在 $\Omicron(\lg n)$ 时间内确认任何的顺序统计量。以及如何在O(lgn)时间内得到一个元素的秩，即它在集合线性序中的位置。

下图展示了一种支持快速顺序统计的数据结构，顺序统计树。这种数据结构是在红黑树的基础上，给每个元素添加一个属性size。一个结点的size表示以这个结点为根结点的子树大小。我们定义哨兵T.nil的size为0，则有如下等式

x.size = x.left.size + x.right.size + 1

动态顺序统计量

查看给定秩的元素

从根结点开始查找，首先通过左孩子的size+1得到当前结点为根节点时的秩r，然后和需要查找的秩i作比较。如果相等则直接返回，如果i < r 查看左孩子，否则递归查看右孩子，但是查看右孩子时，需要传入i - r，因为右子树并不能知道左子树的大小，而右孩子实际的轶为r+右孩子为根结点时的右孩子的秩：

RANK(x.right) = RANK(x) + (x.right.left.size + 1)

查看给定元素的秩

查看一个元素的秩

假如一个元素x的父结点为根结点，
当这个元素x是根结点的左孩子时， $RANK(x) = x.left.size + 1$
当这个元素x是根结点的右孩子时， $RANK(x) = RANK(x.p) + x.left.size + 1$

利用上面的性质，求解一个元素x的秩时，我们循环的求解当x的父结点为根结点时，x在这个子树中的大小，每次循环上移一层，直到移动到真实的root结点，这时我们已经求出了该元素真实的秩。

查看一个元素的秩

维护size

当插入/删除元素时，除了维护红黑树的特性，我们还要维护结点的size属性。正常的插入/删除导致的size变化比较简单，不在赘述。我们看看当发生旋转时size的维护：

维护size

当对x做左旋后，我们需要重新计算x的size，并且把x之前的size赋给y，因为旋转不会影响这个局部子树的size。
当对y做右旋后，我们需要重新计算y的size，同理把y之前的size赋给x。

如何扩张数据结构

扩张一种数据结构可以分为4个步骤：

选择一种基础数据结构
确定基础数据结构中要维护的附加信息
检验基础数据结构上的基本修改操作能否维护附加信息
设计一些新操作

在扩张数据结构时，不一定非得时上述结构，上述只是一个一般模式。但我们可以把上述步骤作为一个check list来检验扩张数据结构是否完善。

区间树

有些问题可能会涉及到区间数据，这时候可能就需要用到区间树。比如：查看某一时间段内发生的事。

我们把一个区间[l, h]表示成一个对象i，i.low = l为低端点，i.high = h为高端点。
下图展示了两个区间的三种状态：

a，区间i和区间i’重叠
b，区间i在区间i’的左边（i.h < i’.l）
c，区间i在区间i’的右边（i.l > i’.h）

区间树是一种对红黑树扩展的数据结构，我们看看红黑树扩展为区间树的过程：

基础数据结构
选择红黑树，每个元素包含区间属性x.int，x的key为x.int.low。
附加信息
每个结点除了区间信息外，包含一个值x.max，它表示以x为根结点子树中所有端点的最大值。
对信息的维护
在插入/删除操作后，需要对max值做维护，最多影响树高h个元素的max值，而且每次维护只需要常数次操作。所以不会影响原有操作的时间复杂度。

x.max = max(x.int.high, x.left.max, x.right.max)
设计新的操作
新操作INTERVAL-SEARCH(T, i)，用来查找区间树T中与区间i重叠的结点。若树中没有区间与i重叠，则返回T.nil。

区间树

INTERVAL-SEARCH(T, i)：将x指向root结点开始循环查看x是否与i重叠，如果重叠则退出循环返回x。如果x有左孩子且左孩子的max值大于等于i.low，则循环查看x的左孩子，否则循环查看x的右结点。

TODO: 用循环不变式证明各个扩张的正确性

留言與分享

13. 红黑树

2015 年 3 月 7 日分類算法

13. 红黑树

二叉搜索树的各种操作时间复杂度为 $\Omicron(h)$ ，但是树的高度h不可控，最差的情况为n。
而平衡搜索树能将树的高度控制在 $\Omicron(\lg(n))$ 。
常见的平衡搜索树有：

AVL树
红黑树
treap （tree + heap，给每个元素随机的priority，从而间接的实现随机插入，使得树的期望高度为 $\Omicron(\lg(n))$ ）
B树（十八章介绍）
- 2-3-4树

本章重点讨论红黑树，以及习题中出现的AVL树。AVL树较为简单所以先介绍AVL树。

AVL树

AVL树由Adel’son-Vel’skii & Landis 在1962年发明，由他们的名字命名。
比较一般的二叉搜索树，每个结点额外存储它的高度，nil的高度为0，其他节点的高度为Height(x) = max(Height(x->left), Height(x->right)) + 1。每个结点两个孩子的高度差不能超过1。
当右子树的高度比左子树的高度高时，我们称right-heavy（如下图），反之这称left-heavy。

AVL树

AVL树的各种查询操作都和普通二叉搜索树无异，所以我们只需关注会改变树结构的Insert操作和Delete操作。
在一般的Insert或者Delete操作后，结点的高度会变，所以有可能会违反AVL树的性质，这时候我们需要引入一个操作Rotate（旋转）

Rotate

旋转分为两种，左旋（LEFT-ROTATE）和右旋（RIGHT-ROTATE）。下图右测变为左侧的情况称为对x结点左旋，左侧变为右侧的情况称为对y结点做右旋。

Rotate

我们可以发现旋转操作并不会影响二叉搜索树的性质。
旋转前后都会保持α <= x <= β <= y <= γ
下面是左旋的伪代码，右旋的操作和左旋对称，不再赘述。

Rotate

Ref：AVLTree::LeftRotate & AVLTree::RightRotate in AVLTree.h

AVL树平衡调整（ADJUST_FROM(x)）

当Insert或者Delete一个元素后，平衡有可能被破坏，假设x是最底层被破坏性质的节点，而且是right-heavy时（left-heavy是对称的）：

Balance
- 如果x的右孩子y是平衡的或者right-heavy的（Figure 5）
  - 我们对x做LEFT-ROTATE操作可使其恢复平衡
  - 然后重新计算x和y的高度
- 如果x的右孩子z是left-heavy的（Figure 6）
  - 我们先对z做RIGHT_ROTATE，然后对x做LEFT-ROTATE，可使其恢复平衡
  - 然后重新计算x，y，z的高度
Loop
- 重新计算x的高度，并使得x=x->p继续循环，直到根节点
- 若图中发现某节点不平衡的用1. Balance

AVL树

Ref：AVLTree::AdjustFrom in AVLTree.h

AVL树 Insert

因为插入的节点肯定是叶子节点，所以直接对插入节点调用ADJUST_FROM(x)即可。

Ref：AVLTree::Insert in AVLTree.h

AVL树 Delete

删除操作略为复杂，可能会影响子节点的平衡。

当被删除节点只有一个孩子，或者没有孩子时，被删除节点的孩子不会被应用
- 这时对删除节点原来的父节点调用ADJUST_FROM(x)即可
当被删除节点有两个孩子时
- 如果被删除节点右子树的最小节点min的父节点为被删除节点，这时对min调用ADJUST_FROM(x)
- 其他情况，对min原来的父节点调用ADJUST_FROM(x)

Ref：AVLTree::Delete in AVLTree.h

红黑树

红黑树也是一种平衡二叉树。它在每个节点上增加一个存储位color来表示节点的颜色，节点的颜色为RED或者BLACK。通过对任何一条从根节点到叶子节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出2倍，所以是近似于平衡的。
红黑树还定义一种NIL节点，NIL节点是红黑树的叶子结点（外部节点），真实的数据组成树的内部节点（如下图a所示）。
红黑树的具体性质如下：

每个节点不是红色的就是黑色的
根节点是黑色的
每个叶结点（NIL）是黑色的
如果一个结点是红色的，那么它的两个孩子都是黑色的
对于每个结点，从该结点到其所有后代叶结点的简单路径上，黑色结点的数量相同

为了方便处理，使用一个哨兵来替代NIL结点。对于一颗红黑树T，哨兵T.nil是一个普通结点。它的color为BLACK，用哨兵T.nil替换图a中的所有NIL，这样就形如下图b所示，T.nil的p, left, right, key属性我们并不关心，所以方便起见程序中可以对其值随意设定。

红黑树

为了方便起见，我们在图中省去T.nil，这样就变成了图c的样子。

NULL -> T.nil

红黑树与普通二叉搜索树相比，用T.nil替代了空指针。
所以所有操作中用到空指针的地方，需要换成T.nil。后面不做赘述。

红黑树 Insert

红黑树的插入操作，除了一般的操作外，还需要把插入结点的颜色设为RED。因为插入了一个红色的结点，所以有可能触犯红黑树的一些性质（1,4），所以我们要调用RB-INSERT-FIXUP将其修正。

红黑树Insert

RB-INSERT-FIXUP会循环的查看z的父结点是否违反性质4，如果违反，则将其修正。如果修正后仍然有可能违反性质4，则继续循环查看其爷结点。（本文只讨论插入结点的父结点为爷结点的左孩子的情况，右孩子的情况与其对称，不再赘述。）

修正过程有三种情况：

Case 1. z的叔结点为红色
Case 2. z的叔结点为黑色，且z是父亲的右孩子
Case 3. z的叔结点为黑色，且z是父亲的左孩子

上图插入4之后的处理过程。下面我们详细讨论下三种情况的处理方式：

Case 1
这种情况只需改变着色，将父节点和叔结点染成黑色，爷结点染成红色。
因为爷结点以前是黑色，却染成了红色，如果爷结点的父结点为红色，这时仍会触犯性质4，所以我们将爷结点赋给z，下次循环时再修正它。
如果z的爷结点为root结点，我们修正后root结点变成了红色，并且让z指向root结点然后跳出了循环。在循环外边我们会将z重新染成黑色，所以保持了性质1。
Case 2/3
当z是父结点的左孩子时，符合Case 3，这时我们只需把爷结点做右旋，然后交换之前父结点和爷结点的颜色。这时局部的根节点颜色没有改变，仍然是黑色，所以整个树都满足了红黑树的特性，无需继续循环。

当z是父结点的右孩子时，符合Case 2，这时只需要对父结点做左旋，使其变为Case 3的情况。

由上可知，一旦循环进入Case 2或者Case 3，就会结束循环。所以一次插入操作最多只会有两次旋转操作。尽量少的循环操作是非常有益的，因为改变结点颜色并不会影响查找功能，当多线程处理时我们只需给旋转操作加锁。

红黑树 Delete

删除操作比插入操作略微复杂，当删除一个黑色结点，或者删除过程中移动了一个黑色结点时，都有可能破坏红黑树的性质（2,4,5）。

当被删除的结点只有一个孩子，或者没有孩子，这时我们只需关心被删除结点的颜色，如果被删除的结点为红色，则无需修正，如果被删除结点为黑色，则需要从被删除结点的孩子开始修正。

当被删除的结点有两个孩子时，我们会找右子树的最小结点来替代被删除结点的位置和颜色，所以这是我们需要关注这个最小结点的颜色，如果最小结点的颜色为红色，则无需修整，如果这个最小结点为黑色，则需要从最小结点的右孩子开始修正。

红黑树Delete

从x开始修正时，有五种情况：

Case 0. x为红色
- 这时23行会将其设为黑色，可直接满足所有红黑树性质
Case 1. x的兄弟结点w为红色
Case 2. x的兄弟节点w为黑色，且w的两个孩子都是黑色
Case 3. x的兄弟节点w为黑色，且w的右孩子为黑色，左孩子有红色
Case 4. x的兄弟节点w为黑色，且w的右孩子为红色

红黑树Insert

Case 1
这种情况我们将其转换为Case2/3/4
1. 设置兄弟节点w为黑色，父结点为红色
2. 左旋父结点
3. 重新设置w为x的兄弟结点
Case 2
这种情况将兄弟结点w设置为红色，并且x=x.p，继续循环。
我们会发现，如果是从Case 1转换到Case 2，那么x.p一定是红色，所以会直接退出循环。
Case 3
这种情况我们将其转换为Case4
1. 设置兄弟节点w为红色，w的左孩子为黑色
2. 右旋w结点
3. 重新设置w为x的兄弟结点
Case 4
这种情况可以做一些修改，然后结束修正
1. 设置w的颜色为x父结点的颜色
2. x父结点的颜色设置为黑色
3. w右孩子的颜色设置为黑色
4. 左旋x的父结点
5. 使x指向root结点，从而结束修正

由上可知，一旦循环进入Case 1, Case 3，Case 4，就会结束循环。所以一次插入操作最多只会有三次旋转操作（Case 1 -> Case 3 -> Case 4）。

性质维护:

插入过程中维护性质的分析：

1 2	Case1 转换后，局部的黑高与之前相同但是由于将局部根节点C从黑色变成红色，所以需要继续考虑C是否违反性质4

1 2	Case2/3 转换后，局部的黑高与之前相同并且局部根节点B的颜色没有改变，所以直接Done

删除过程中维护性质的分析：

需要修正时，被修正结点x以前的父节点肯定为黑色，x替代了x以前父节点的位置
所以这时这个子树（x为根节点）的黑高减少了1

Case1 转换后，ABCDE的黑高都没有变
所以这时仍然是x为根节点的子树黑高少1

根本情况没有变化，变化的只是x的兄弟节点的颜色

Case2 转换后，以x的父节点c为根节点的子树已经满足红黑树的性质
但是c为根节点的子树的黑高比之前少1

所以令c为新的x，继续调整

Case3 转换后，ABCDE的黑高都没有变
所以这时仍然是x为根节点的子树黑高少1

根本情况没有变化，变化的只是w的右孩子的颜色

Case4 转换后，以c为根节点子树满足红黑树性质
并且根节点的颜色没有变化，子树的黑高也没有变化

所以Done

涉及数据结构

点击查看实现

AVL树
红黑树

留言與分享

12. 二叉搜索树

2015 年 3 月 6 日分類算法

12. 二叉搜索树

二叉搜索树支持许多动态集合的操作，包括Search，Insert，Delete，Minimum，Maximum，Successor，Predecessor。所有操作的时间复杂度为 $\Omicron(h)$ ，h为树的高度。

二叉搜索树

二叉搜索树是一个链式存储的二叉树，且具有如下特性：
设x为二叉搜索树中的一个结点。

如果y是x左子树中的一个结点，那么y.key<=x.key。
如果y是x右子树中的一个结点，那么y.key>=x.key。

二叉搜索树

Search

从根节点开始查找，如果查询的k小于根节点的key，则递归查找左子树；如果查询的k大于根节点的key，则递归查找右子树；如果查询的k等于根节点的key，done。

Minimum

从根节点开始沿着left child方向一直找到低。

Minimum

Maximum

从根节点开始沿着right child方向一直找到低。

Maximum

Successor & Predecessor

查询x的下一个节点：

如果x有右孩子，那么x的下一个节点就是右子树的最小值。
1
2
3
4
5
6
7
○
/ \
●
/ \
○
/ \
[○]
若果x没有右孩子，那么x的下一个节点是x的第n个parent，这个parent是第一个符合下图的情况，第n-1个parent 是第n个parent得 left child。
1
2
3
4
5
6
[○]
/ \
○
/ \
●
/
如果没有符合这样情况的parent，那么说明x是最大数，没有下一个节点。

Successor

Insert

上图描述了插入key为13的数据。
从根节点x开始查找。如果待插入数据小于该节点数据，到左子树继续查找，否则到右子树查找，直到找到一个空位置，将数据放入。

Insert

Delete

删除操作的情况较为复杂，有如下几种情况

待删除节点没有孩子
待删除节点只有一个孩子，如下图(a) (b)情况
待删除节点有两个孩子，并且右孩子有左孩子时，如下图(d)情况

Delete

当待删除节点没有孩子时：
- 可以直接删除该节点，并且修改他的父节点，用nil代替他
当待删除节点只有一个孩子时，如图中 (a) (b) 情况：
- 可以直接用子节点替换该节点
当待删除节点有两个孩子时，如图中 © (d) 情况：
- 思路：用待删除节点z的Successor节点y替代它的位置
- 情况c，右孩子没有左孩子（y是z的子节点）
  - y替换z，并且接管z的左孩子
- 情况d，右孩子有左孩子
  - y的右孩子x替换y，并且y接管z的右孩子
  - y替换z，并且接管z的左孩子

Delete
Delete

Tips：当待删除节点有两个孩子时，用待删除节点的Predecessor节点替代它也可以。

涉及数据结构

点击查看实现

二叉搜索树

留言與分享

下一頁
第 1 頁共 3 頁

mysql基础教程

数据模型

数据类型

主流关系数据库

SQL

DDL：Data Definition Language

DML：Data Manipulation Language

DQL：Data Query Language

语法特点

MariaDB

Aurora

PolarDB

安装MySQL

使用Docker运行MySQL

关系模型

主键

联合主键

小结

多对多

一对一

小结

唯一索引

小结

准备数据

MySQL

基本查询

小结

常用的条件表达式

小结

投影查询

小结

排序

排序

小结

注意

思考

小结

分组

练习

小结

小结

小结

插入数据

小结

MySQL

小结

删除数据

MySQL

小结

MySQL

小结

数据库

表

退出MySQL

插入或替换

插入或更新

插入或忽略

快照

写入查询结果集

强制使用指定索引

事务

隔离级别

小结

Read Uncommitted

Read Committed

Repeatable Read

默认隔离级别

pandas 快速入门

pandas 快速入门#

pandas 中的基本数据结构#

对象创建#

查看数据#

选择#

Getitem ([])#

按标签选择#

按位置选择#

布尔索引#

设置#

缺失数据#

操作#

Getitem (`[]`)#