不是有个叫迪杰斯特拉(Dijkstra)的算法吗?名字难记不说,加权图的最短路径问题在实际开发中也很少需要自己实现,所以总是很快就忘了。。。
迪杰斯特拉算法是什么
迪杰斯特拉算法是一种用于求解图的最短路径的算法。很多人可能只是听过这个名字。虽然它的原理简单易懂,但初次接触可能有些难以理解,不过只要逐步分析就会发现它其实是一个相当直观的算法。
对于没有权重的迷宫搜索等问题,可以用广度优先搜索(BFS)解决,但如果每条边都有权重,就需要计算所有可能的路径。假设每个顶点只经过一次,且有E条边,那么时间复杂度会是O(E!),计算量会爆炸式增长。
这样计算起来就很不现实。
而迪杰斯特拉算法正是高效解决这类问题的算法。
需要注意的是,各边的成本必须是非负值(大于等于0)。如果包含负数,则需要使用贝尔曼-福特(Bellman-Ford)等算法。
步骤
迪杰斯特拉算法的步骤非常简单:
- 将起点的最短距离设为0
- 从未访问的点中选择已知最短距离且距离最小的顶点移动
- 设置该顶点连接的其他顶点的最短距离。如果可以更新更短的距离,则更新。
- 重复以上步骤,直到所有顶点的最短距离都确定
光这么说可能有点抽象,下面我们通过一个具体例子来说明。
示例
虽然方法很原始,但这是最能表达清楚的方式…
我们来看下面这张图的最短路径:
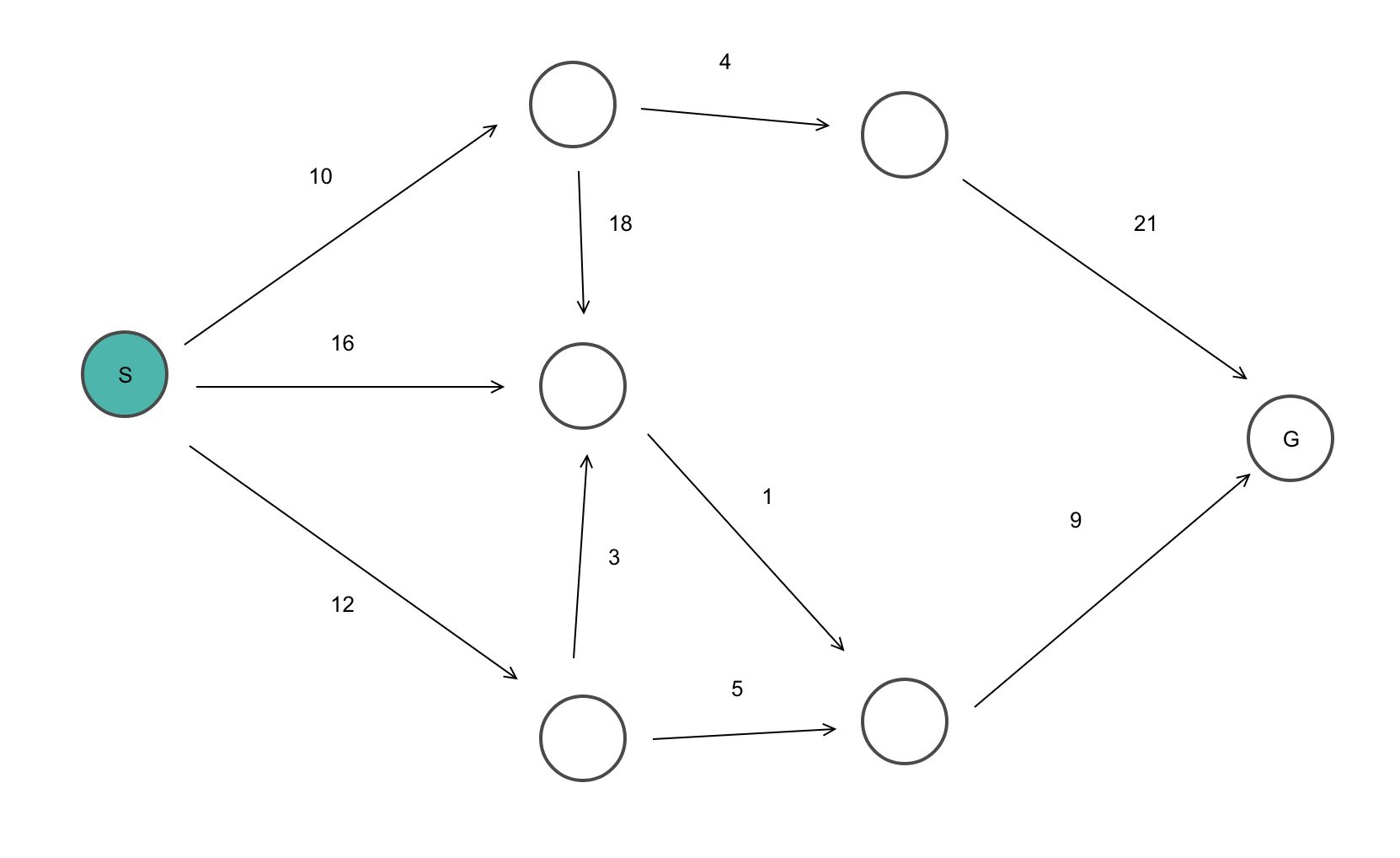
绿色表示最短路径已确定并已访问的顶点,红色是起点顶点。每个顶点上的数字表示当前的最短路径:

可以看到,算法从起点开始,每次移动到当前最短路径的顶点,并计算相邻顶点的最短路径。
实现
接下来我们来实现这个算法。
按照上述步骤直接实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| function main(nodes) {
const start = nodes[0]
const visited = new Set()
const routesFromStart = new Map()
routesFromStart.set(start, {distance: 0})
for(const n of nodes) {
if(n != start) {
routesFromStart.set(n, {distance: Number.MAX_VALUE})
}
}
let current = start
let routes = new Map()
while(current != null) {
visited.add(current)
for(const edge of current.edges) {
if(edge.cost + routesFromStart.get(current).distance < routesFromStart.get(edge.to).distance) {
routesFromStart.set(edge.to, {distance: edge.cost + routesFromStart.get(current).distance})
routes.set(current, edge.to)
}
}
let cheapestNodeDistance = Number.MAX_VALUE
current = null
for(const city of routesFromStart.keys()) {
if(!visited.has(city) && cheapestNodeDistance > routesFromStart.get(city).distance){
cheapestNodeDistance = routesFromStart.get(city).distance
current = city
}
}
}
return routesFromStart.get(nodes[nodes.length - 1]).distance
}
|
假设顶点数为V,这段代码在最坏情况下需要遍历所有边,并在内部循环中选择最小顶点,因此时间复杂度是O(V² + E)。空间复杂度需要记录每个顶点,所以是O(V)。
关于使用优先队列的实现
细心的读者可能已经发现,这段代码中选取最小顶点的逻辑可以优化,这就是优先队列(Priority Queue)。
优先队列的插入和取出操作需要O(logN)的时间复杂度,但比线性搜索最小顶点更快。
JavaScript没有内置优先队列,以下是Python实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| def dijkstra(nodes):
start_node = nodes[0]
routes_from_start = {n: math.inf for n in nodes}
routes_from_start[start_node] = 0
minHeap = []
heappush(minHeap, (0, start_node))
while minHeap:
(cost, current_node) = heappop(minHeap)
if cost > routes_from_start[current_node]:
continue
for node in current_node.routes:
price_info = current_node.routes[node]
if routes_from_start[node] > price_info + routes_from_start[current_node]:
routes_from_start[node] = price_info + routes_from_start[current_node]
heappush(minHeap, (price_info + routes_from_start[current_node], node))
return routes_from_start[nodes[-1]]
|
优先队列的说明我们以后再讨论。
优化后的算法时间复杂度为O(V + ElogE),比最初的实现更高效。
记录路径
现在我们已经能求出最短成本,但这是"最短路径"问题,我们自然还想知道具体路径。
改进上面的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| def dijkstra(nodes):
start_node = nodes[0]
routes_from_start = {n: math.inf for n in nodes}
routes_from_start[start_node] = 0
minHeap = []
heappush(minHeap, (0, start_node))
path = collections.defaultdict(Node)
while minHeap:
(cost, current_node) = heappop(minHeap)
if cost > routes_from_start[current_node]:
continue
for node in current_node.routes:
price_info = current_node.routes[node]
if routes_from_start[node] > price_info + routes_from_start[current_node]:
routes_from_start[node] = price_info + routes_from_start[current_node]
path[node.id] = current_node.id
heappush(minHeap, (price_info + routes_from_start[current_node], node))
current_node = nodes[-1].id
path_array = []
while current_node:
path_array.append(current_node)
if current_node not in path:
break
current_node = path[current_node]
return routes_from_start[nodes[-1]], path_array[::-1]
|
迪杰斯特拉算法会记录更新最短距离的节点,最后回溯即可。时间复杂度会增加最短路径节点数的计算量。
为什么这样能求出最短路径
看到这里,很多人可能会想:算法本身很简单,实现也不难,但为什么能保证求出最短距离呢?我们简单验证一下:
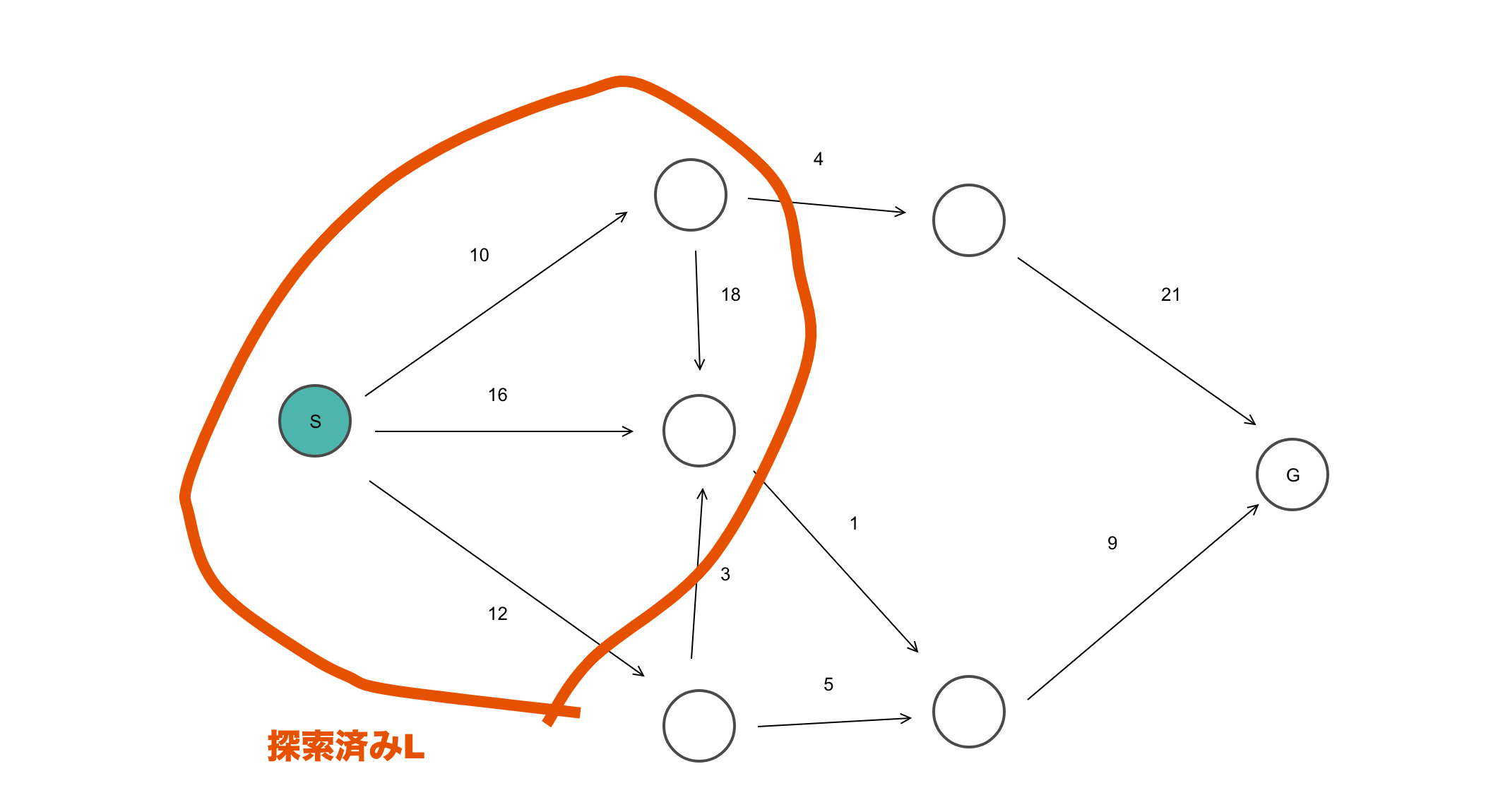
假设集合L中的顶点到起点S的最短距离已确定,那么从L连接到的最小顶点也应该是S的最短距离。
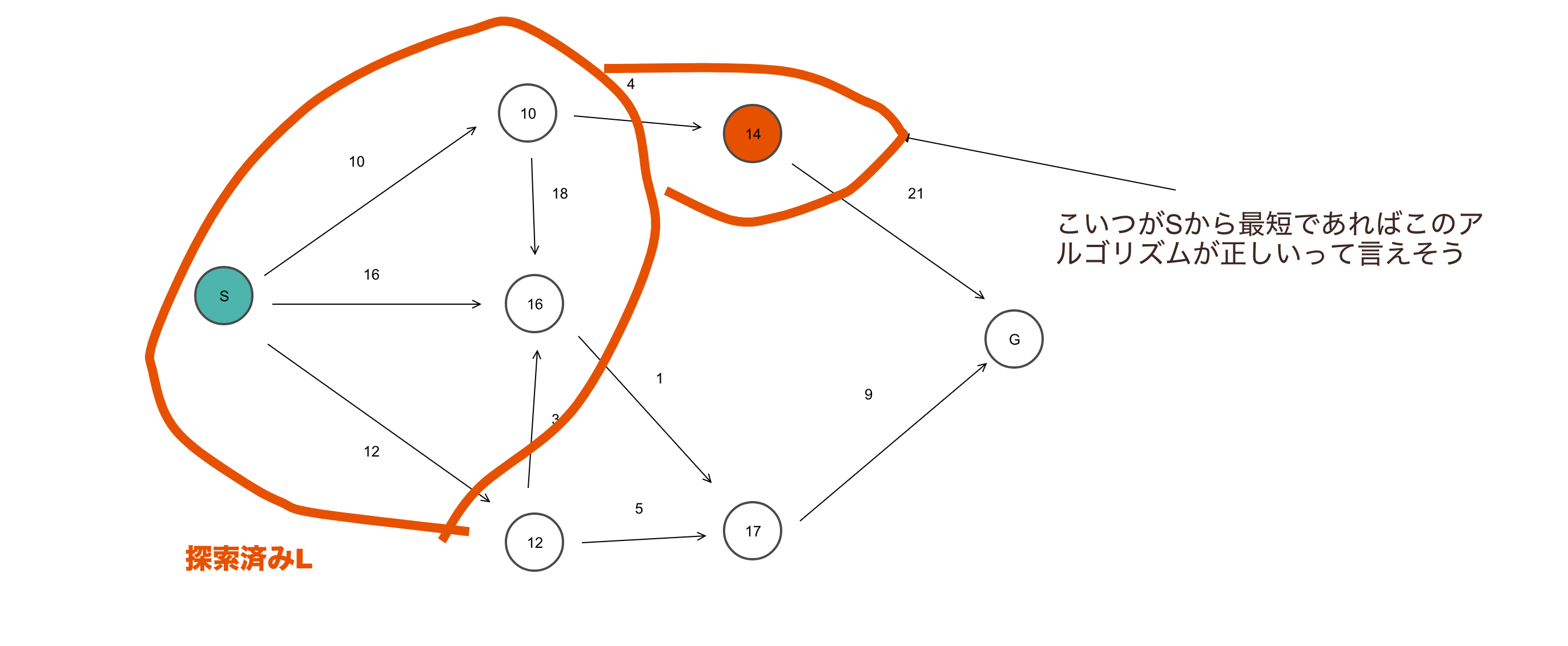
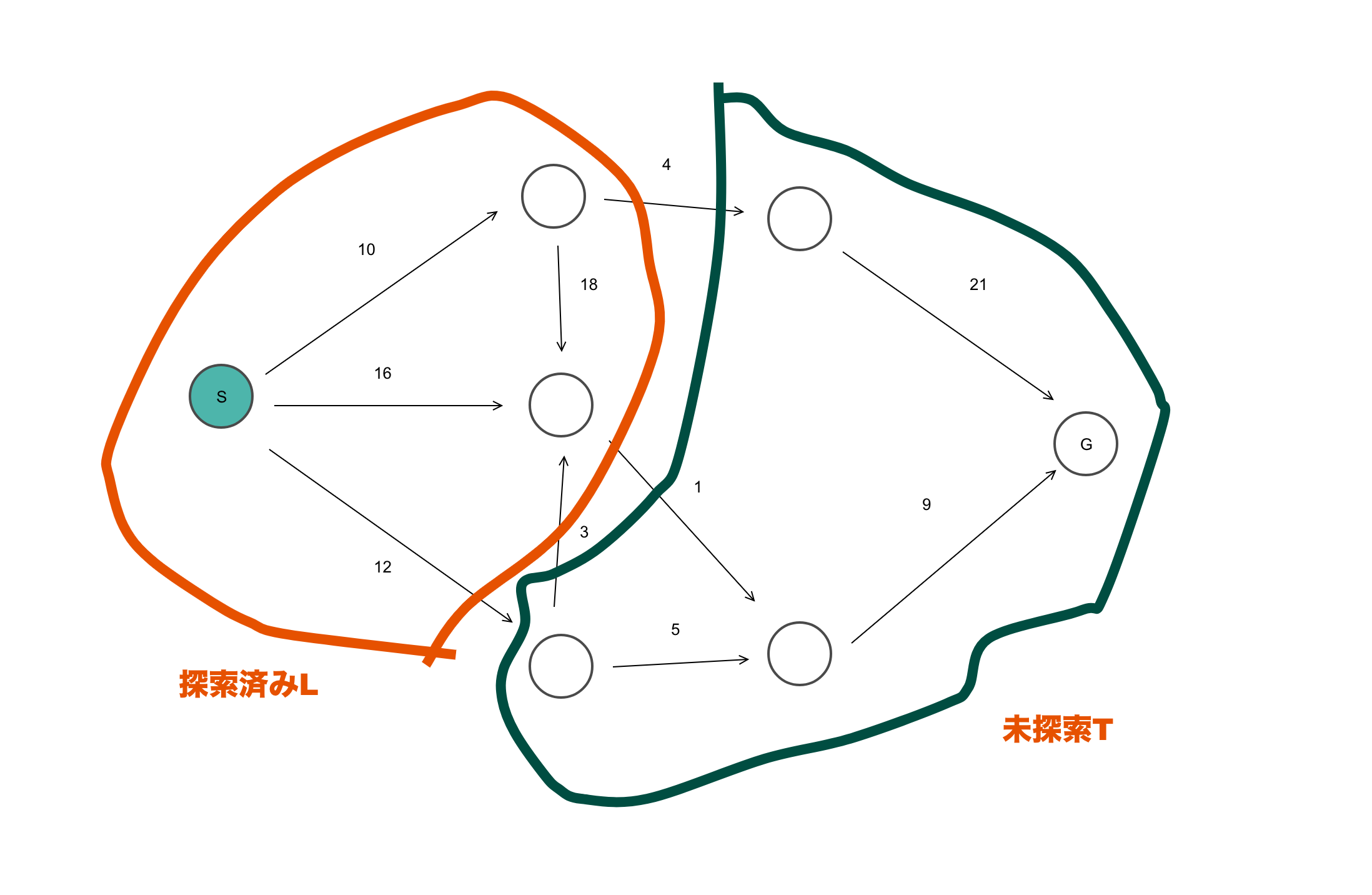
在集合T中选取最小顶点i,则d[i] = min(T)。对于任意顶点k,最短距离d[k] ≥ d[i]是确定的,因为d[i]是最小值且各边权重非负。
通过归纳法可以证明这一点。
其实这就是一个递推公式:
d[i] = min(k ⊂ T) + i到L中相邻顶点的最短距离
说到递推公式就想到动态规划(DP)。关于DP可以参考这篇文章:
https://qiita.com/drken/items/a5e6fe22863b7992efdb
用DP来看值的更新过程:
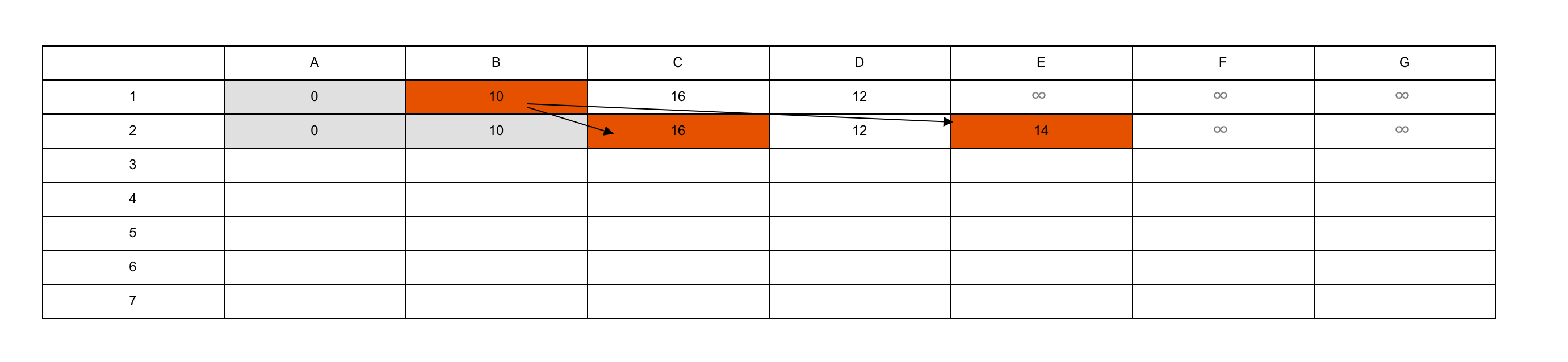
纵轴表示迭代次数,横轴表示顶点。原来迪杰斯特拉算法是DP的一种啊。
总结
通过以上分析,迪杰斯特拉算法一旦理解后其实相当简单。以后在算法问题中遇到类似问题时,希望能快速联想到这个算法。
*顺便说一句,我也想写一篇关于DP的文章
讲解视频可以在这里观看:
https://youtu.be/jz8b0q5R1Ss
参考
http://www.lab2.kuis.kyoto-u.ac.jp/~shuichi/algintro/alg-6s.pdf
https://www.youtube.com/watch?v=X1AsMlJdiok







