R 绘图 - 饼图
R 语言提供来大量的库来实现绘图功能。
饼图,或称饼状图,是一个划分为几个扇形的圆形统计图表,用于描述量、频率或百分比之间的相对关系。
R 语言使用 pie() 函数来实现饼图,语法格式如下:
1
2
3
4
| pie(x, labels = names(x), edges = 200, radius = 0.8,
clockwise = FALSE, init.angle = if(clockwise) 90 else 0,
density = NULL, angle = 45, col = NULL, border = NULL,
lty = NULL, main = NULL, …)
|
- x: 数值向量,表示每个扇形的面积。
- labels: 字符型向量,表示各扇形面积标签。
- edges: 这个参数用处不大,指的是多边形的边数(圆的轮廓类似很多边的多边形)。
- radius: 饼图的半径。
- main: 饼图的标题。
- clockwise: 是一个逻辑值,用来指示饼图各个切片是否按顺时针做出分割。
- angle: 设置底纹的斜率。
- density: 底纹的密度。默认值为 NULL。
- col: 是表示每个扇形的颜色,相当于调色板。
绘制饼状图要做这些准备:反映数量的向量、各部分的标签、各部分的颜色(可选)。
接下来我们绘制一个简单的饼图:
实例
1
2
3
4
5
6
7
8
9
10
11
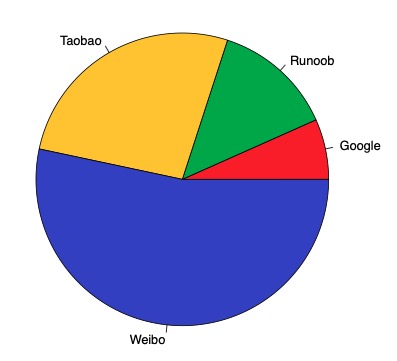
| \# 数据准备
info = c(1, 2, 4, 8)
\# 命名
names = c("Google", "Runoob", "Taobao", "Weibo")
\# 涂色(可选)
cols = c("#ED1C24","#22B14C","#FFC90E","#3f48CC")
\# 绘图
pie(info, labels\=names, col\=cols)
|
执行绘图程序,会在当前目录下生存一个 PDF 文件(Rplots.pdf),打开文件可以看到图形效果如下:
我们也可以使用 png()、jpeg()、bmp() 函数设置输出的文件格式为图片:
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
| \# 数据准备
info \= c(1, 2, 4, 8)
\# 命名
names \= c("Google", "Runoob", "Taobao", "Weibo")
\# 涂色(可选)
cols \= c("#ED1C24","#22B14C","#FFC90E","#3f48CC")
\# 设置输出图片
png(file\='runoob-pie.png', height\=300, width\=300)
\# 绘图
pie(info, labels\=names, col\=cols)
|
接下来我们给饼图设置标题,中文字体需要设置字体参数 family=‘GB1’,也可以自己设置字体库,详细参考:R 绘图 - 中文支持。
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
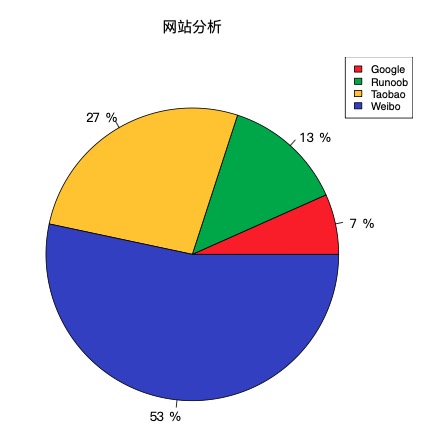
| \# 数据准备
info = c(1, 2, 4, 8)
\# 命名
names = c("Google", "Runoob", "Taobao", "Weibo")
\# 涂色(可选)
cols = c("#ED1C24","#22B14C","#FFC90E","#3f48CC")
\# 计算百分比
piepercent = paste(round(100\*info/sum(info)), "%")
\# 绘图
pie(info, labels\=piepercent, main = "网站分析", col\=cols, family\='GB1')
\# 添加颜色样本标注
legend("topright", names, cex\=0.8, fill\=cols)
|
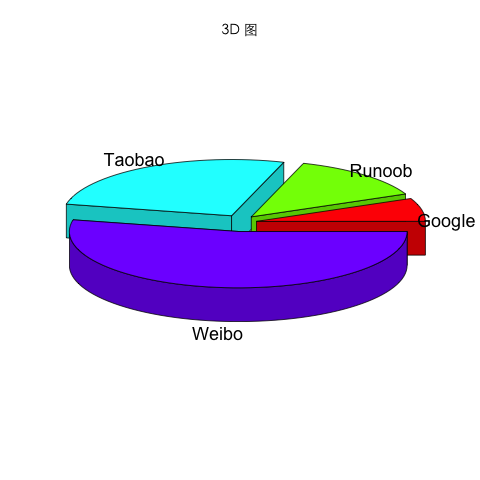
如果要绘制 3D 的饼图,可以使用 plotrix 库的 pie3D() 函数,使用前我们需要先安装:
1
| install.packages("plotrix", repos = "https://mirrors.ustc.edu.cn/CRAN/")
|
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| \# 载入 plotrix
library(plotrix)
\# 数据准备
info \= c(1, 2, 4, 8)
\# 命名
names \= c("Google", "Runoob", "Taobao", "Weibo")
\# 涂色(可选)
cols \= c("#ED1C24","#22B14C","#FFC90E","#3f48CC")
\# 设置文件名,输出为 png
png(file \= "3d\_pie\_chart.png")
\# 绘制 3D 图,family 要设置你系统支持的中文字体库
pie3D(info,labels \= names,explode \= 0.1, main \= "3D 图",family \= "STHeitiTC-Light")
|
生成图片如下所示:
R 绘图 - 条形图
条形图,也称为柱状图条形图,是一种以长方形的长度为变量的统计图表。
条形图可以是水平或垂直的,每个长方形可以有不同的颜色。
R 语言使用 barplot() 函数来创建条形图,格式如下:
1
| barplot(H,xlab,ylab,main, names.arg,col,beside)
|
参数说明:
- H 向量或矩阵,包含图表用的数字值,每个数值表示矩形条的高度。
- xlab x 轴标签。
- ylab y 轴标签。
- main 图表标题。
- names.arg 每个矩形条的名称。
- col 每个矩形条的颜色。
接下来我们创建一个简单的条形图:
实例
1
2
3
4
5
| \# 准备一个向量
cvd19 \= c(83534,2640626,585493)
\# 显示条形图
barplot(cvd19)
|
执行绘图程序,会在当前目录下生存一个 PDF 文件(Rplots.pdf),打开文件可以看到图形效果如下:
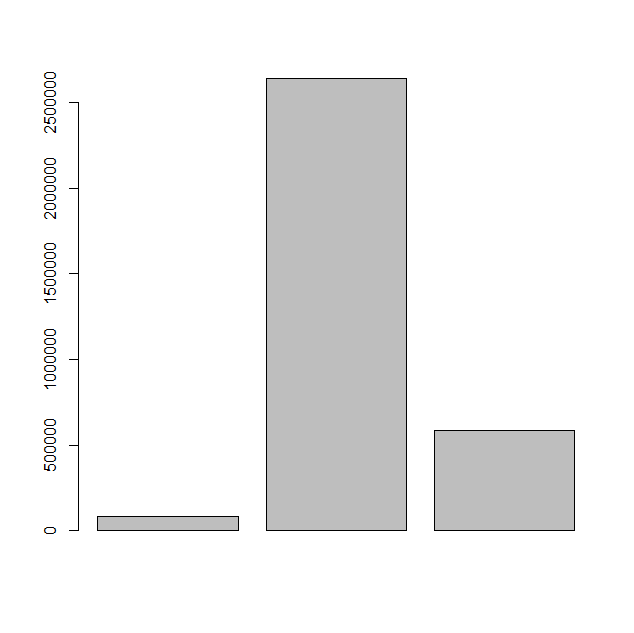
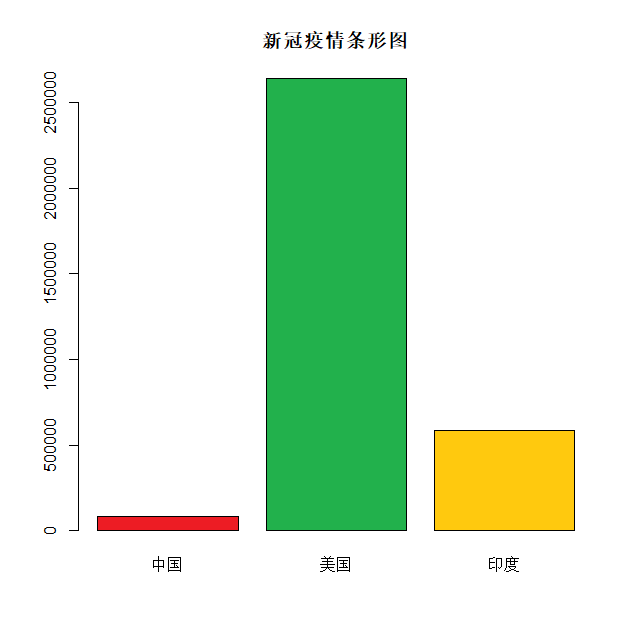
为了更好地表达信息,我们可以在图表上添加标题、颜色及每个矩形条的名称。
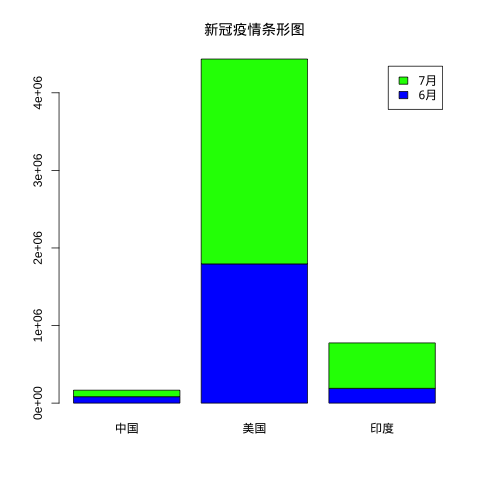
以下我们创建 2020 年 7 月 1 日中国、美国和印度的新冠疫情确诊人数统计图。
中文字体需要设置字体参数 family=‘GB1’:
实例
1
2
3
4
5
6
7
8
| cvd19 \= c(83534,2640626,585493)
barplot(cvd19,
main\="新冠疫情条形图",
col\=c("#ED1C24","#22B14C","#FFC90E"),
names.arg\=c("中国","美国","印度"),
family\='GB1'
)
|
barplot 中的数据既可以是向量,也可以是矩阵,现在我们生成一张新冠疫情 6 月和 7 月对比图。
首先准备数据:
|
中国 |
美国 |
印度 |
| 6 月 |
83017 |
1794546 |
190535 |
| 7 月 |
83534 |
2640626 |
585493 |
转换成矩阵,生成条形图,按并排格式显示,而且要显示颜色样本。
这里我们设置了自己的字体库,详细内容可以参考 R 绘图 - 中文支持
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| library(showtext);
font\_add("SyHei", "SourceHanSansSC-Bold.otf");
cvd19 \= matrix(
c(83017, 83534, 1794546, 2640626, 190535, 585493),
2, 3
)
\# 设置文件名,输出为 png
png(file \= "runoob-bar-1.png")
#加载字体
showtext\_begin();
colnames(cvd19) \= c("中国", "美国", "印度")
rownames(cvd19) \= c("6月", "7月")
barplot(cvd19, main \= "新冠疫情条形图", beside\=TRUE, legend\=TRUE, family\='SyHei')
\# 去掉字体
showtext\_end();
|
以下代码会在当前程序目录下生存一个 runoob-bar-1.png 文件,如下所示:
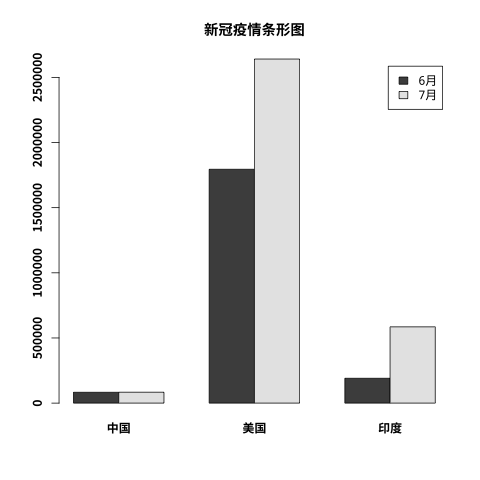
我们设置的颜色样本将是每各组的颜色样本:
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| library(plotrix)
library(showtext);
font\_add("SyHei", "SourceHanSansSC-Bold.otf");
cvd19 \= matrix(
c(83017, 83534, 1794546, 2640626, 190535, 585493),
2, 3
)
\# 设置文件名,输出为 png
png(file \= "runoob-bar-2.png")
#加载字体
showtext\_begin();
colnames(cvd19) \= c("中国", "美国", "印度")
rownames(cvd19) \= c("6月", "7月")
barplot(cvd19, main \= "新冠疫情条形图", beside\=TRUE, legend\=TRUE,col\=c("blue","green"), family\='SyHei')
\# 去掉字体
showtext\_end();
|
以下代码会在当前程序目录下生存一个 runoob-bar-2.png 文件,如下所示:
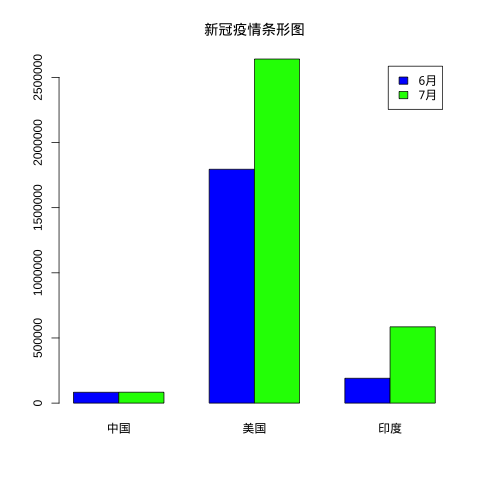
beside 参数
beside 设置矩形条堆叠的方式,默认为 FALSE:
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| library(showtext);
font\_add("SyHei", "SourceHanSansSC-Bold.otf");
cvd19 \= matrix(
c(83017, 83534, 1794546, 2640626, 190535, 585493),
2, 3
)
\# 设置文件名,输出为 png
png(file \= "runoob-bar-3.png")
#加载字体
showtext\_begin();
colnames(cvd19) \= c("中国", "美国", "印度")
rownames(cvd19) \= c("6月", "7月")
barplot(cvd19, main \= "新冠疫情条形图", beside\=FALSE, legend\=TRUE,col\=c("blue","green"), family\='SyHei')
\# 去掉字体
showtext\_end();
|
以下代码会在当前程序目录下生存一个 runoob-bar-3.png 文件,如下所示:
R 绘图 - 函数曲线图
函数曲线图是研究函数的重要工具。
R 中 curve() 函数可以绘制函数的图像,代码格式如下:
1
2
3
4
5
6
| curve(expr, from = NULL, to = NULL, n = 101, add = FALSE,
type = "l", xname = "x", xlab = xname, ylab = NULL,
log = NULL, xlim = NULL, …)
# S3 函数的方法
plot(x, y = 0, to = 1, from = y, xlim = NULL, ylab = NULL, …)
|
**注:**R 语言的类有 S3 类和 S4 类,S3 类用的比较广,创建简单粗糙但是灵活,而 S4 类比较精细。
参数:
- expr:函数表达式
- from 和 to:绘图的起止范围
- n:一个整数值,表示 x 取值的数量
- add:是一个逻辑值,当为 TRUE 时,表示将绘图添加到已存在的绘图中。
- type:绘图的类型,p 为点、l 为直线, o 同时绘制点和线,且线穿过点。
- xname:用于 x 轴变量的名称。
- xlim 和 ylim 表示x轴和y轴的范围。
- xlab,ylab:x 轴和 y 轴的标签名称。
plot 函数中,x 和 y 分别表示所绘图形的横坐标和纵坐标。
以下我们绘制一个 sin(x) 函数的图表:
1
| curve(sin(x), -2 * pi, 2 * pi)
|
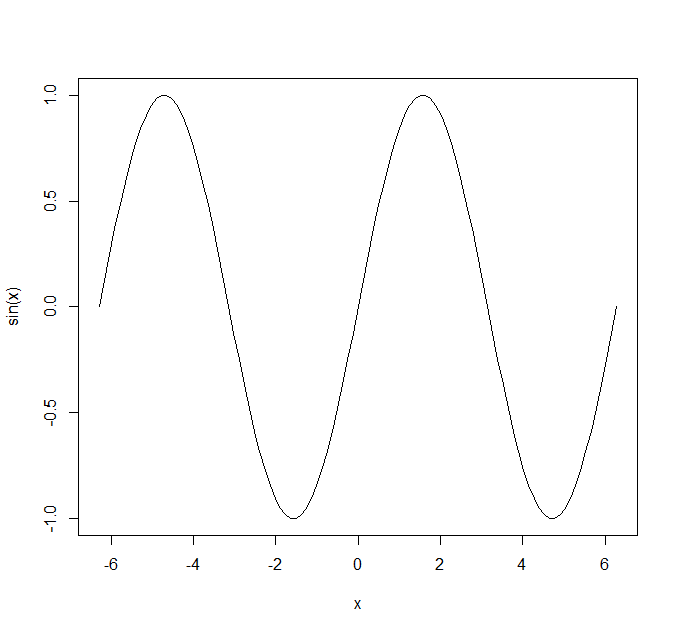
注意:任何计算机绘图工具绘制的都是模式图,它并不能保证与真的函数图像一模一样,它只是每隔一段距离取一个点,然后计算这个点的"高度"并绘制出来,为了保证曲线连续性,相邻两个点之间会有直线连接,所以在某些情况下例如 tan(x) 可能会出现错误:
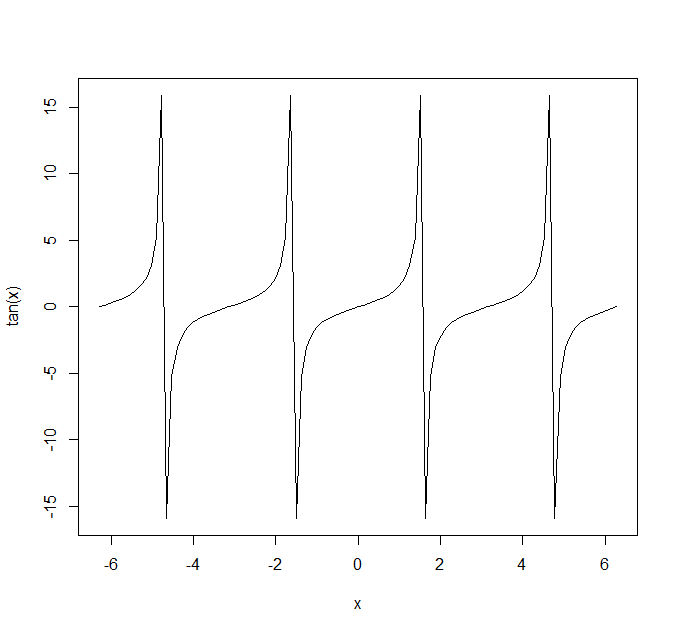
在每一个 (2n+1)Pi / 2 的位置都会出现断点,但是 R 的图像将它们连接了,希望大家理解这一点。
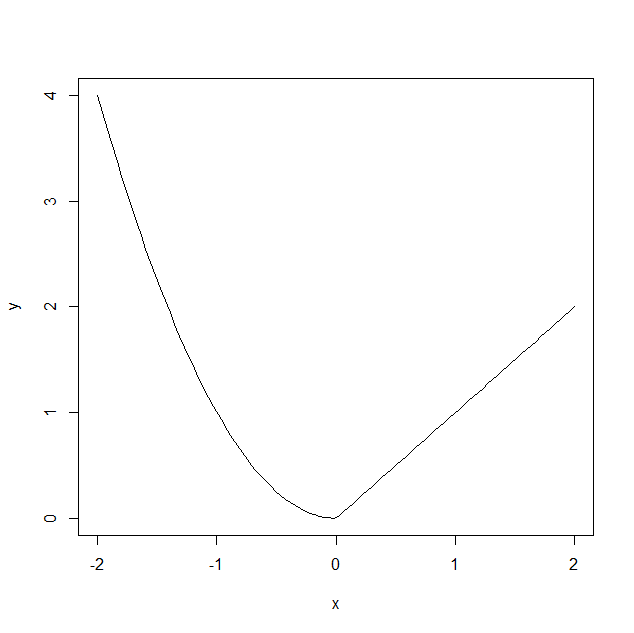
当然,不是所有的函数都像 sin 一样支持向量处理,我们也可以手动生成一个数字序列然后用 plot 函数生成函数图像。假设函数 f 仅支持单个数值作为参数:
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| \# 定义函数 f
f \= function (x) {
if (x \>= 0) {
x
} else {
x ^ 2
}
}
\# 生成自变量序列
x \= seq(\-2, 2, length\=100)
\# 生成因变量序列
y \= rep(0, length(x))
j \= 1
for (i in x) {
y\[j\] \= f(i)
j \= j + 1
}
\# 绘制图像
plot(x, y, type\='l')
|
接下来我们使用 plot() 函数对向量数据进行绘图:
实例
1
2
3
4
5
6
7
8
9
| \# 向量数据
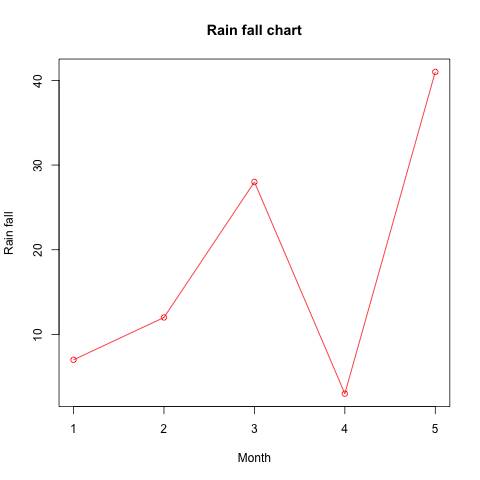
v <- c(7,12,28,3,41)
\# 生成图片
png(file \= "line\_chart\_label\_colored.jpg")
\# 绘图、线图颜色为红色,main 参数用于设置标题
plot(v,type \= "o", col \= "red", xlab \= "Month", ylab \= "Rain fall",
main \= "Rain fall chart")
|
R 绘图 - 散点图
散点图是将所有的数据以点的形式展现在直角坐标系上,以显示变量之间的相互影响程度,点的位置由变量的数值决定,每个点对应一个 X 和 Y 轴点坐标。
散点图可以使用 plot() 函数来绘制,语法格式如下:
1
| plot(x, y, type="p", main, xlab, ylab, xlim, ylim, axes)
|
type 参数可选择值:
- p:点图
- l:线图
- b:同时绘制点和线
- c:仅绘制参数 b 所示的线
- o:同时绘制点和线,且线穿过点
- h:绘制出点到横坐标轴的垂直线
- s:阶梯图,先横后纵
- S:阶梯图,先纵后竖
- n: 空图
创建一个简单的线图:
实例
1
2
3
4
5
6
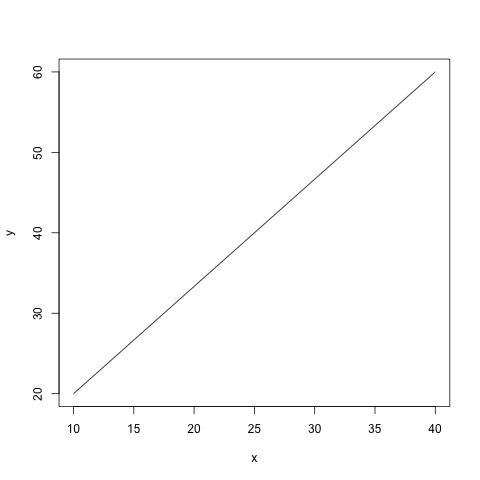
| x<-c(10,40)
y<-c(20,60)
\# 生成 png 图片
png(file \= "runnob-test-plot2.png")
plot(x, y, "l")
|
创建一个简单的线图,type 使用 o 参数,同时绘制点和线,且线穿过点:
实例
1
2
3
4
5
6
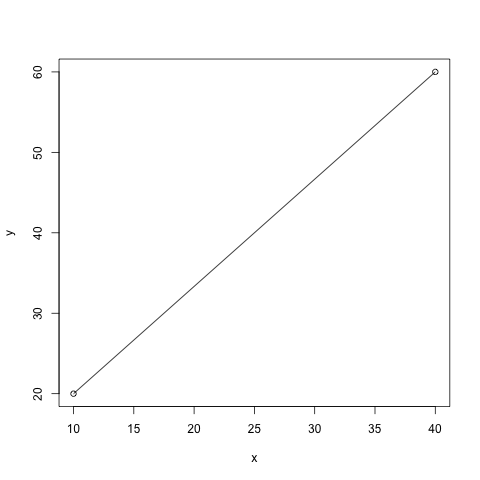
| x<-c(10,40)
y<-c(20,60)
\# 生成 png 图片
png(file \= "runnob-test-plot.png")
plot(x, y, "o")
|
接下来我们使用 R 语言的内置数据集 mtcars 来进行测试。
我们使用 mtcars 数据集的 wt 和 mpg 列:
实例
1
2
| input <- mtcars\[,c('wt','mpg')\]
print(head(input))
|
输出结果为:
1
2
3
4
5
6
7
| wt mpg
Mazda RX4 2.620 21.0
Mazda RX4 Wag 2.875 21.0
Datsun 710 2.320 22.8
Hornet 4 Drive 3.215 21.4
Hornet Sportabout 3.440 18.7
Valiant 3.460 18.1
|
接着我们使用以上数据生存一个散点图
:
实例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
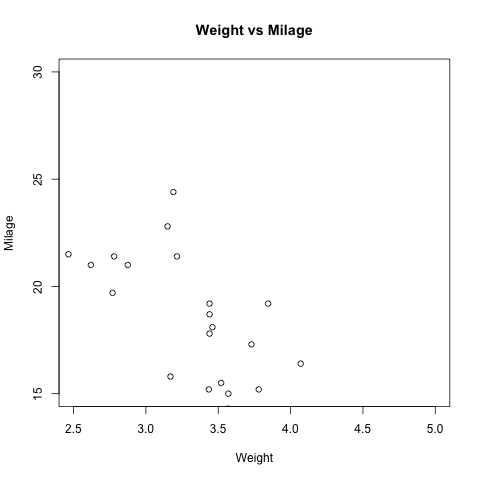
| \# 数据
input <- mtcars\[,c('wt','mpg')\]
\# 生成 png 图片
png(file \= "scatterplot.png")
\# 设置坐标 x 轴范围 2.5 到 5, y 轴范围 15 到 30.
plot(x \= input$wt,y \= input$mpg,
xlab \= "Weight",
ylab \= "Milage",
xlim \= c(2.5,5),
ylim \= c(15,30),
main \= "Weight vs Milage"
)
|
散点图矩阵
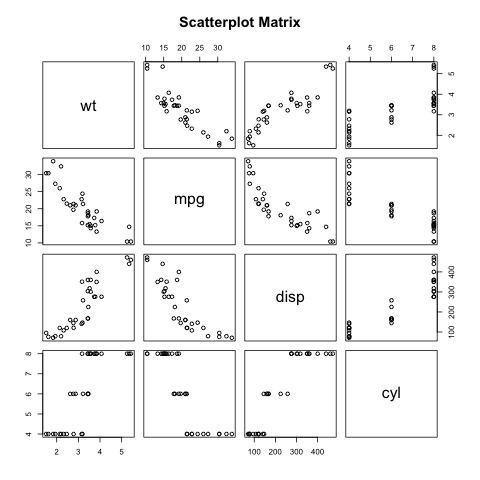
散点图矩阵是借助两变量散点图的作图方法,它可以看作是一个大的图形方阵,其每一个非主对角元素的位置上是对应行的变量与对应列的变量的散点图。而主对角元素位置上是各变量名,这样,借助散点图矩阵可以清晰地看到所研究多个变量两两之间的相关关系。
散点图矩阵就是把数据集中的每个数值变量两两绘制散点图。
R 语言使用以下函数创建散点图矩阵:
参数:
实例
1
2
3
4
5
6
| \# 输出图片
png(file \= "scatterplot\_matrices.png")
\# 4 个变量绘制矩阵,12 个图
pairs(~wt+mpg+disp+cyl,data \= mtcars, main \= "Scatterplot Matrix")
|